La documentation sur ce intéressant des tests optiques récents est apparu sur Internet dans les différentes langues des pays où il est la construction optique auto-amateur plus répandue. Ainsi, un texte en italien, il n'y a pas actuellement. C’est pour ca que, des curieux et “initiés” Je pensais que de traduire en italien, Je l'utilise et les gens comme moi qui peuvent en bénéficier, L'article suivant, dont l'original est situé à l'adresse suivante: http://www.astrosurf.com/tests/roddier/roddier.htm
L'avantage de ce test est qu'il est de photométrie de type, puis il fournit des informations sur l'état de la surface optique miroir ENTIER. Mais cette information ne sont pas le résultat des évaluations subjectives en exécutant le test, comme avec presque tous les tests optiques amateurs applicables, mais ils sont le résultat d'une évaluation objective effectuée par l'ordinateur sur la base de deux séances de photos réalisées sur l'image d'un tir étoiles à focale intra et extra par l'instrument.
Le fait, cependant, que ce test intéressant est basé sur deux plans de caméra à l'intérieur et à l'extérieur d'un foyer du télescope, On suppose que le télescope est un outil déjà construite et opérationnelle.
Ce qui relègue l'utilisation de l'intérêt de test dans une simple évaluation qualitative d'une optique existante, rendant inutile le fabricant “gratte verre” qui aspire toujours à trouver une alternative à l'évaluation objective la subjectivité inhérente plus ou moins dans tous les tests utilisés dans le parabolizzazione en perspective, visant à fournir un guide quantitatif pour les corrections à apporter à divers réglages qui se succèdent sur le chemin de la fabrication “meilleur miroir”, se non “parfait”.
Ceci est un test “sous-produit” de la technologie”l'optique adaptative”, développé, (et pour un certain temps “classifié” avec intérêt militaire) pour déformer localement et temporairement les propriétés optiques de très grands télescopes afin de compenser instantanément des dommages causés par la turbulence atmosphérique, éliminant pratiquement ce dernier en temps réel, comme cela se produit au cours de l'observation.
Une telle optique adaptative prévoit la transformation de l'image capturée par le télescope dans un algorithme mathématique qui identifie la présence d'une certaine aberration optique local, et la correction d'actionneurs mécaniques qui génèrent un signe opposé.
L'étude des aberrations optiques, et leur description en termes mathématiques grandement facilitée par l'informatique, Cela signifie que le même principe peut être appliqué dans ce test RODDIER pour l'évaluation de l'optique également au niveau amateur, avec une précision et l'exhaustivité intéressante.
Voici l'article:
(Claude et son mari François Roddier ont travaillé à l'observatoire à Hawaï, en particulier sur la haute résolution angulaire. Ils sont maintenant à la retraite. Leurs travaux sur l'optique et d'adaptation actifs ont contribué à l'amélioration de la performance des très grands télescopes. )
1. Principe théorique
2. Un exemple pour mieux comprendre
3. Un exemple pratique
Comme il est connu, avec le test visuel de type test étoile, vous pouvez obtenir des informations sur les défauts optiques d'un instrument, observant les deux images floues d'une étoile. Le test Roddier généralise ce concept avec un programme informatique réalisant une analyse géométrique et photométrie deux photographies automatiques exécutées en intra et extrafocal, obtenu avec une caméra CCD.
• Le programme informatique est disponible gratuitement sur le Web
• Voir l'état d'avancement du projet visant à relier l'article original indiqué ci-dessus, et télécharger le programme WinRoddier.
1. Principe théorique
Pour commencer, nous considérons un outil parfait, il fournit à son attention l'image d'une étoile. Ils ont ensuite enregistré deux images defocalizzate; une heure à la distance « l » avant , sur le feu (vers l'intérieur de l'instrument); et une fois dans le même « l », mais la distance de retour devant le feu (vers l'extérieur de l'instrument)
La pupille d'entrée est éclairée de manière uniforme (intensité I0 ), et juste une petite partie de cet élève (Fig. 1): Le flux lumineux passant à travers cette petite portion intrafocale éclaire l'image sur une surface inférieure, avec une intensité I1, et l'image extrafocal sur une surface I2 égale à celle de l'image intrafocale, étant donné que les deux images sont prises à la même distance du feu. L'intensité initiale I0 est donc « concentré » de la même manière sur les deux images, et vous avez:
I1 = I2
Supposons maintenant que le front de l'onde sortant de la pupille d'entrée a un défaut: Sur la surface de petite pupille précédemment considérée, il apparaît courbé (fig.2) .Le feu est réel, pour cette portion de la pupille, situé en face du feu de l'instrument. Sur l'image intrafocale ainsi, la lumière est plus concentrée que sur le extrafocal.
I1 > I2
Col di essai est Roddier compare maintenant I1 à I2 grâce au calcul de la quantité I2 - I1, pour revenir aux défauts dans le front d'onde.

figue. 2 : Test Roddier d'un instrument défectueux: L'intensité de l'I1et I2 sont différents. Cette différence d'intensité est liée à la courbure du front d'onde.
La théorie montre que si l'on considère l'image dans son ensemble (et non petites portions comme ci-dessus), le signal calculé en effectuant la soustraction des deux images intra et extra, Elle est proportionnelle au Laplacien du front d'onde.
• Le Laplacien front d'onde (le calcul de ce qui implique la dérivée seconde), Elle est liée à la courbure du front d'onde (voir la figure 2)
NOTE: (l'opérateur mathématique ou Laplace Laplacien, dont le nom est dû à Pierre Simon Laplace, est un second opérateur différentiel d'ordre défini comme la divergence du gradient d'une fonction dans un espace euclidien).
Le problème dans notre cas est différent: Nous devons reconstruire le front d'onde de son laplacien. Cela se fait avec l'aide d'un programme informatique spécialisé, marques, en plus du calcul du Laplacien, de nombreuses corrections géométriques et photométriques visant à déterminer les aberrations de front d'onde.
Ces calculs sont souvent effectués en temps réel par les professionnels (Active dans les systèmes optiques modernes, ou adaptatif) l'exécution de l'Roddier d'essai afin de déformer la surface optique des grands miroirs afin de corriger les aberrations du front d'onde.
2. Un exemple pour mieux comprendre
La figure 3 Elle représente la zone de feu d'un outil bosselé de l'aberration sphérique (en overcorrection) : Les rayons centraux convergent avec une distance focale plus courte que celle des rayons marginaux. L'aberration de front d'onde correspondant à cela se traduit par des niveaux de gris (figue. 4A): Le front d'onde est concave au milieu, et répliqué au niveau du bord. L'image de la figure 4B représente le laplacien de ce front d'onde.

figue. 3 : région d'incendie d'un outil présentant une aberration sphérique (sur-correction). La carte cible a une longueur focale plus longue que celle de son centre. mots-clés + e – se référer aux différences d'intensité lumineuse sur les images intra et extra, par rapport à une intensité uniformément répartie en l'absence d'aberration (le cas de la figure 1).

Fig.4A: Wavefront – Figura 4B: Laplacien front d'onde – Fig.5 A. photo intrafocale – La figure 5B. photo extrafocal
Considérons maintenant les images intra et extra de la figure 5
• Situation centrale des images : En intra il y a un excès d'intensité (note +) et extras il y a un défaut (note -) parce que les rayons centraux convergent plus proche de l'image intra (Voir image 3).
• Zone image marginale : En intra il y a une intensité de défaut (remarqué le signe -) tout en supplémentaire il y a excès (remarqué le signe +) parce que les rayons marginaux convergent plus proche de l'image supplémentaire (Voir image 3).
Quand il réalise la soustraction des deux images S, vous obtenez les résultats suivants:
• Zone centrale : Un excès d'intensité (+) – (-) = (+)
• zone marginale : Un défaut d'intensité que (-) – (+) = (-)
C'est en fait ce que nous observons sur l'image Laplacien front d'onde (figura 4B).
Le front d'onde est liée laplacien, S au signal obtenu en soustrayant les deux images intra et extra .
(Ce que nous avons vu jusqu'à présent est ici une illustration simple pour fixer les idées, qui est, en aucun cas une manifestation !)
3. Un exemple pratique
Une fois que nous avons pris des mesures pour reconstruire le front d'onde, on peut faire remonter aux valeurs des principales aberrations de décomposition de la même front d'onde polynômes de Zernike.
Ces polynômes sont des fonctions mathématiques définies sur un disque, qui peut être lié aux grandes aberrations.
Par exemple,, l'image de la figure 4 est la représentation du polynôme de Zernike est lié à l'aberration sphérique (lire plus de détails sur les polynômes Zernike). Ajout de plus polynômes, vous pouvez reconstruire une aberration de front d'onde le plus touché par. inversement, un front d'onde mesurées peut être ajusté à différents polynômes, afin de détecter les aberrations.
À titre d'exemple, nous reproduisons ici un extrait de l'analyse d'un commerce Schmidt-Cassegrain (bonne qualité). 5A est l'image du front d'onde reconstruit à partir programme informatique EF à partir de deux images intra et focales supplémentaires.
Ce qui suit table 1 Il affiche les valeurs RMS de une aberration, et la figure 5B est l'image du front d'onde reconstruit en utilisant les valeurs des aberrations et de la 22 premiers polynômes de Zernike. L'utilisation de ces 22 polynômes vous permet de trouver les principales aberrations et reconstruire la forme générale du front d'onde.
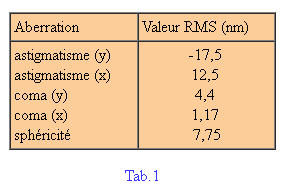
Fig.5A: Front d'onde calculé avec le programme EF à partir d'une image intrafocale et d'une
extrafocale.
Fig.5B: Wavefront reconstruit à partir de 22 les polynômes sont Zernike, utilisant des valeurs efficaces
aberrations fournies par le programme EF.
Le tableau 1 est un extrait de ces 22 titres. (L'unité de mesure est le nanomètre).
(NOTE: Autres explications intéressantes et trouver des logiciels mis à jour sur le Web en recherchant: “Projet WinRoddier” votre Astrosurf – et discussion “Test optique (Roddier)” sul forum Nuit nuageuse).

