The subject self-build a telescope, at a certain point of its progression it leads to make concatenated choices, where the pupil of the eye conditions the determination of the minimum magnification with an eyepiece "telescope finder" or wide field; from which it is derived the design of the full light field" (Field Of View) be prepared, and therefore the choice of the type of focuser if 1.25 "or 2", and finally it determines the size of the secondary mirror.
Everything has a price, and from these choices it is conditioned in a direct way also the final weight of the instrument with which must then make the accounts of adequate balancing and / or ease of transport.
Our passion for astronomy leads us to observe the wonders of the sky through the use of binoculars or telescopes, to whom we have a thousand cures, they will achieve the best possible performance. In this intent, it happens often (and it happened to me), only belatedly taking into account that the human eye is first an optical instrument, Perhaps less well known than it is our telescope. Rather, the eye is the target of the largest optical instrument that we possess, with its own strengths and unfortunately also its many flaws.
Leaving aside the vision defects, that are very personal, you can concentrate on the general feature that regulates the performance and the’ “opening” of this particular optical objective, which as such, must let pass through that diaphragm which is the iris, the beam of light that will make up the image on our retina.
The variation of the size of that hole or physiological diaphragm, produce the “entrance pupil” this our natural goal.
E 'it is known that a human being of a young age has an eye whose iris is able to dilate in darkness up to present a pupil 7 mm diametro, which in fact constitutes the highest pupil "entry" young eye. And it is well known that the human pupil, with aging is subject to stenosis that gradually restricts both the speed of adaptation that its maximum expansion in the darkness, coming just over a maximum of about 5mm.
Conversely, in full light the pupil shrinks up to a diameter of approximately 2 mm. Obviously this “entrance pupil” constituted by the eye, it is important that it can allow the passage of the entire beam of light and information, that is provided by a telescope or binoculars or other optical instrument in use.
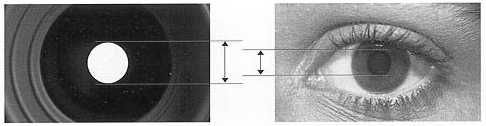
Telescope or binoculars that as such it is well characterized in order to provide an eye his “exit pupil” of a certain size, which it is in fact the diameter of the light beam that it is able to let pass. And it is equal to the diameter of the objective divided by the magnification.
Then: A pair of binoculars with a 50mm lens that provides 8 enlargements will have a diameter of exit pupil (50/8)= 6.25 mm
The entrance pupil of our eye should therefore not ever have smaller diameter than that of the light beam outputted by a tool in use, because in that case (see figure), the eye would lose some of the light, and with it, of the information provided by that optical object.
In other words, losing part of the light provided by the telescope, It is equivalent to physically not being able to use the full opening of its objective. And not be able to use all its opening it is equivalent to looking through a prepunched optical object, that is penalized by our eye.
In a practical example of diaphragmation:
If I, who am no longer young, own eyes with a pupil diameter 5 mm, and my binoculars 8×50 provides an exit pupil of 50/8 = 6.25 mm; In my eyes you could only get a fraction of light equal to 5/6,25 (Only the ’ 80%) of the total light supplied from the binoculars, and then the rest will be lost.
That loss means that for my eye, that binoculars will not present to me the useful aperture of 50mm, but it will be less, namely diaphragmed 80% of the named 50mm, which are 40mm…With the result that through that reduced opening at just 40mm, I will see a picture of 20% (one fifth) darker and less detailed than the one that would see a young man, through my own binoculars.
And this reasoning is very useful to us, to manage the choice of the right eyepieces most performing for us, according to our real pupil.
Which focal length of an equipupillary eyepiece with my telescope will have the maximum efficiency for me?
Let's suppose we have a Newton reflector with a lens diameter of 360mm which has a focal length of 1830mm, and to have measured the pupil of my eye “geriatric” diameter 5mm.
The ratio between the two aperture diameters is the pure number 360/5 = 72 times
I will therefore have to look for an eyepiece that gives me that magnification of 72 times.
Knowing that the magnification given by a telescope is equal to the ratio of the focal length of the objective, divided by the focal length of the eyepiece used; and therefore inversely, that the relationship between the focal length of the telescope and the magnification, it will give me the focal length of the eyepiece.
In my case it will be 1830 mm / 72 = 25 mm, the focal length of best performance.
Any eyepiece with a focal length greater than 25mm will provide my eye with an unnecessarily too large beam of light, going unnecessarily to lighten the bottom of the sky by decreasing the contrast.
That said, for each of us, might be interesting to measure the amplitude of our pupil dilated and accustomed to dark.
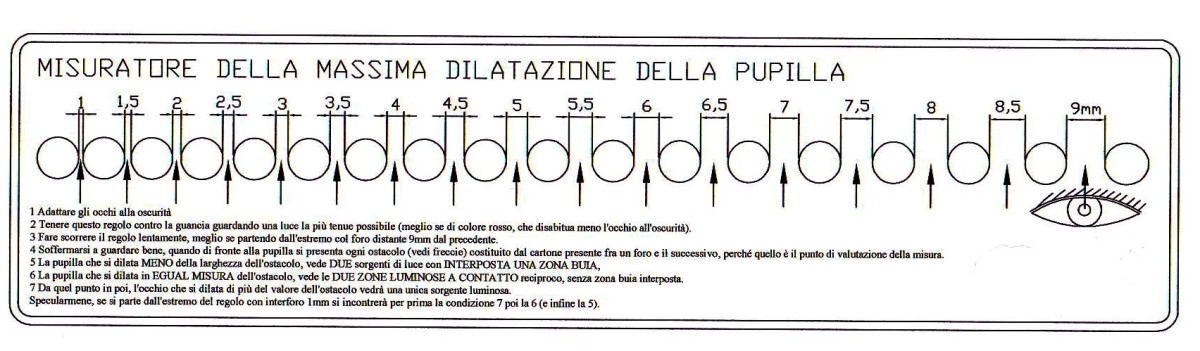
To play in homemade so this measurement, is possible to print and fabricate and use, the following rule in cardboard, whose operating principle is similar to that of professional counterparts pupillometers instruments denominated test pupil of Krusius, Morton, etc.
This cardboard slide rule is to be printed to scale 1:1 1:1 and cut out opening 18 holes, verifying that the print measures correspond to the actual measurements of the distances between the various holes.
The ruler is used as follows:
- 1) Adjust your eyes to the darkness
- 2) Hold the ruler in contact with the face in front of the eye, and look through the holes a light the most tenuous possible (preferably red or reddish, which it is a clolor which has the property of not disturbing the eye's adaptation to darkness).
- 3) Slide the ruler slowly, BETTER STARTING FROM THE FAR RIGHT that have the hole distant 9 mm from the previous.
- 4) Pausing to look good when in front of the pupil occurs every obstacle constituted by this cardboard between a hole and the other, because that is the extent of the evaluation point (on the ruler, indicated by an arrows upwards).
- 5) Case 1: The pupil that dilates LESS than the width of the obstacle:, looks TWO light sources with AN INTERMEDIATE DARK ZONE.
- 6) Case 2: The pupil that dilates equally by the obstacle:, mans no more sees interposed dark zone where are the obstacle, but it see two bright areas in contact one with each other. The pupil dilation in this case would have exactly equal to the distance of the obstacle that is between the two adjacent holes.
- 7) From that point onard, the eye that expands more than the value of the obstacle will see a single light source.
Starting instead from the left of the ruler, which presents the most large obstacle 1 mm, will meet first the condition 7 , and then 6 and the other in descent.