Dimensionnement du barillet (miroir primaire cellule) avec GUI PLOP

QUOI GUI PLOP:

PLOP GUI est un programme puissant pour l’évaluation de projet et de la qualité du barillet, a savoir de la cellule de montage du miroir primaire du télescope.

Pourquoi peut être critique la mécanique de support du barillet du miroir primaire?

Qui est de la profession, est conscient du fait que l'optique de précision d'une lentille de télescope réflecteur pour la qualité “juste acceptable”, Il consiste à présenter un défaut SUR LE VERRE de sa surface réfléchissante (compris comme mesure “pic sur vallèe (crête à creux)” de sa pire rugosité de surface), telle qui ne dépasse pas 68,75 nanomètres, ou millionièmes de millimètre, qui dégradent l'’ ONDE REFLECHIE D'une valeur d’un quatrième de la longueur d’onde (lambda) de 550 nanomètres possédée par la lumière réfléchie de couleur jaune-vert, à laquelle l'œil humain est plus sensible: C'est la célèbre “lambda / 4.

Et cela est dû au fait que l'onde, Elle se traduit par, Il est endommagé deux fois par un erreur sur le verre: Une premiere fois a l'incidence avec le miroir, et une seconde fois au moment de emerger du verre..   

Et ce double accident et l'action des vagues émergents montre que, pour maintenir sur l'onde un defaut de réflexion de Lambda/4 , il faut sur le verre posséder une double précision, à savoir Lambda / 8, Depuis que:

Lambda / 8 + Lambda / 8 = lambda / 4.

De toute évidence, car il est d'atteindre au moins la précision des 68.75 millionièmes de millimètre de tolérance , les performance du miroir peuvent être considérablement influencé également par des déformations pas propres de l'optique, mais induite at elle par un médiocre support du miroir , que, dans sa cellule peut être déclenché à Flex quand varie ses pointant vers l'observation des objets qui sont au Zénith ou à d’autres qui seront à l’horizon.

Ces possibles flexions irons génèrer une erreur supplémentaire qui est ajoutée à celui de la surface, potentiellement a dégrader la performance de l’instrument.

Qui est il l’auteur de GUI PLOP?

Le programme est le résultat du travail de plusieurs personnes. Comme il est indiqué dans la fenêtre “A propos de Plop”, ceux cités pour la première importance est l'auteur du programme, et David Lewis, ingénieur Toshimi Taki.

Ce dernier est ingénieur en aéronautique japonais avec le passe-temps de l'astronomie, et modifié à cet effet un outil spécifique de designers modernes, C'est a dire la méthode de calcul de structures de «éléments finis» , pour être en mesure d'appliquer pour concevoir et vérifier les cellules de soutien des miroirs pour télescopes, de telle manière à minimiser les distorsions introduites par les contraintes qui affectent négativement les performances optiques.

L'une de ces cellules de soutien en fait, Elle est caractérisée par le miroir primaire de support d'une série de points dans le plan, dont la disposition est calculé afin de charger sur chacune d'entre elles, une partie du poids du miroir aussi pendent la variation de son assiette, par exemple pour générer la distorsion minimale de la réflexion supreficie(en fonction du nombre de points d'appui choisis), et avec cette erreur de distorsion montrer l'erreur de réflexion optique exprimée avec RMS, et aussi dans les valeurs du rapport pic/vallée, qu'iront se chevaucher avec les autres erreurs de surface, contribuer à la dégradation de la performance de l'instrument.

Qu'est-ce que “Calcul de structure par éléments finis”?:

Et l'étude du comportement sous charge d'un complexe d'élément de construction sollicité par ses supports (dans notre cas, le miroir) , qui est ensuite divisée en un réseau de milliers de composants de taille discret, dont le comportement en charge est descriptible avec l'approximation des équations algébriques, seulement avec la puissance des ordinateurs d'aujourd'hui. Les équations qui décrivent, venir à afficher dans différentes couleurs les différents degrés de déformation des différentes zones stressées de la surface en cours d'examen.

A l'astr o amateur a quoi sert GUI PLOP?

Le programme permet des évaluations techniques approfondies qui vont bien au-delà de la connaissance de base de l’astronome amateur bricoleur. Toutefois, en ce qui concerne « do it yourself » amateur astronomique, GUI PLOP est très utile pour le dimensionnement du projet de la cellule principale de votre télescope.

Mais l'utilisation du programme ne sont pas aussi « convivial » et immédiat. Donc, les gens non plus jeunes comme moi, que très rarement utilisent cet logiciel, dans le temps, oublient le «comment faire».

C’est la raison qui me pousse souvent à écrire les instructions «reminder» dans l’intérêt de moi-même. aux quels pouvoir recourir dans le temps en cas de besoin (c'est sur) futur.

Ce matériau est donc un..

 PSEUDO TUTORIEL POUR L'UTILISATION DU LOGICIEL GUI PLOP

…Limité à un exemple pratique de dimensionnement d'une cellule de miroir primaire Newton avec Ø300mm 9 points d'appui (mais nous verrons que a l’utilisateur est toutefois réservé la possibilité de choisir le nombre des points d'appui souhaitable, pour comparer leurs valeurs et choisir celui optimale).

1) Dans la fenetre PLOP CELL DESIGNER, cliquez sur AUTOMATIC CELLE DESIGN –

   

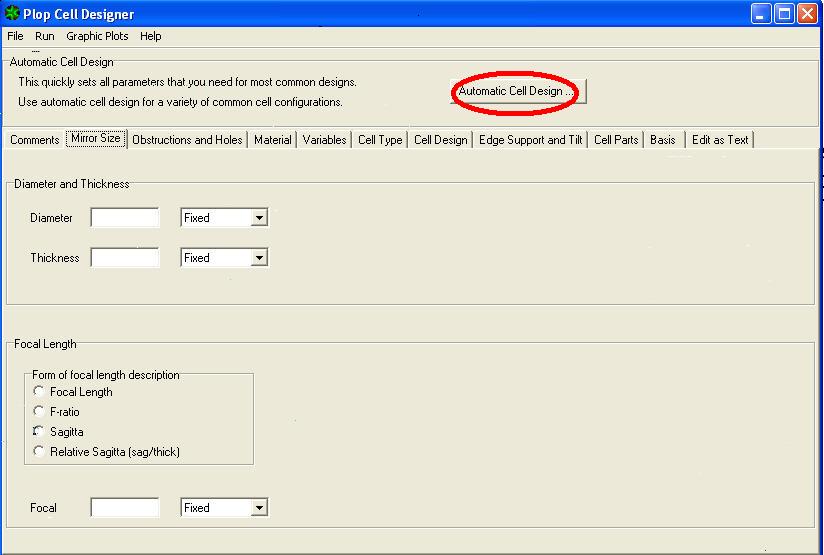
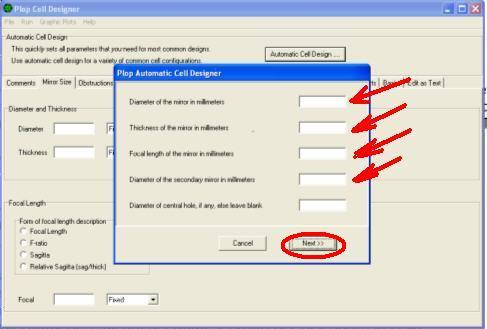
S'ouvre donc la fenêtre PLOP AUTOMATIC CELL DESIGNER, où placer le diamètre primaire 300 mm – 30 mm d'épaisseur – longueur focale 1500mm – diamètre du miroir secondaire 67 mm – pour un miroir Newton, laissez vide le trou centrale –

2) Cliquez sur NEXT –

  

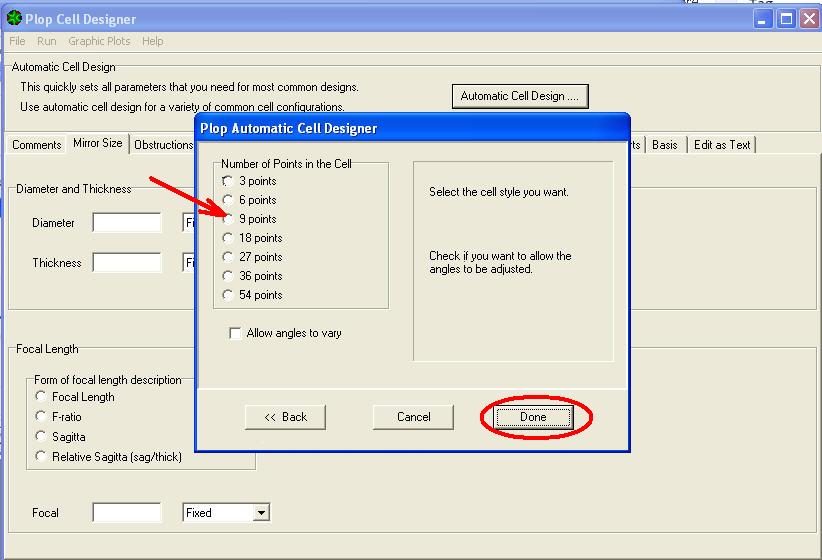
Vous ouvrez la fenêtre pour choisir le numéros des points d’appui de la cellule

3) Choisissez la cellule 9 Point et cliquez sur Terminé (Done)

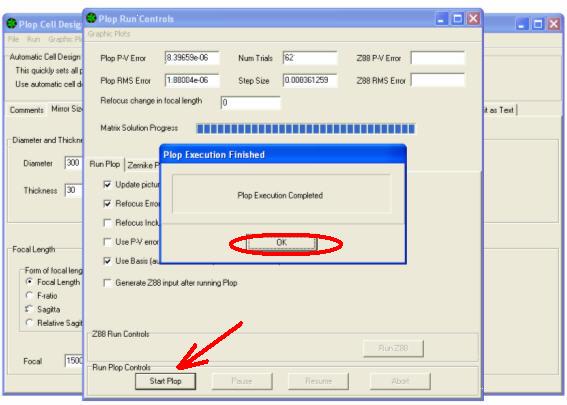
4) Vous ouvrez la fenetre PLOP RUN CONTROLS des commandes exécuter où cliquez sur START PLOP pour commencer à tracer –

le logiciel calcules, et quand il a fini ouvre la fenetre de communication – PLOT EXECUTION FINISHED –

5) appuyez sur OK. La page suivante devient visible , à partir duquel, en cliquant sur l'onglet MODIFIER COMME TEXTE….

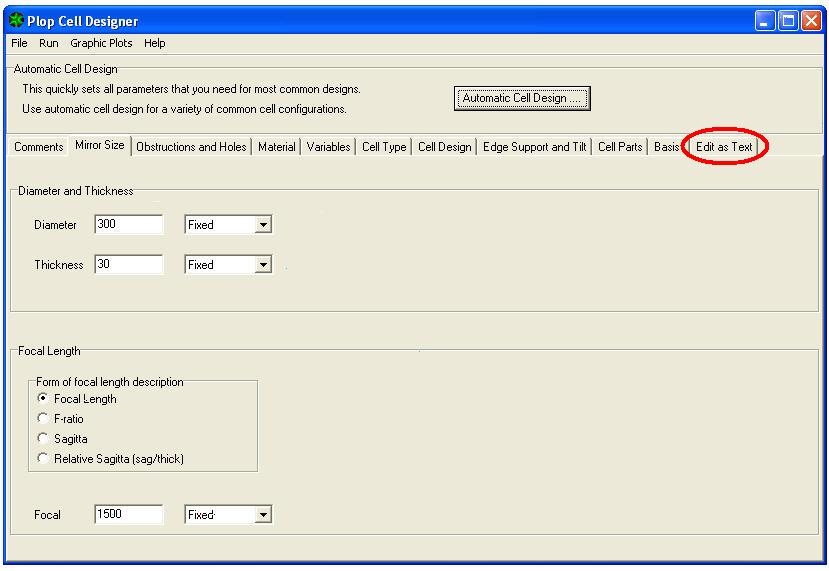
6) la liste suivante des variables et des coefficients de calcul relatifs apparaît dans la moitié inférieure de la page, que multiplié par le diamètre du miroir, fournir les mesures correctes des circonférences intérieures et extérieures, sur lequel ils s'élèveront (pour notre cellule un 9 points) les 3 points d'appui internes, ed les 6 exterieurs triangles supports du miroir dans son barillet.

  

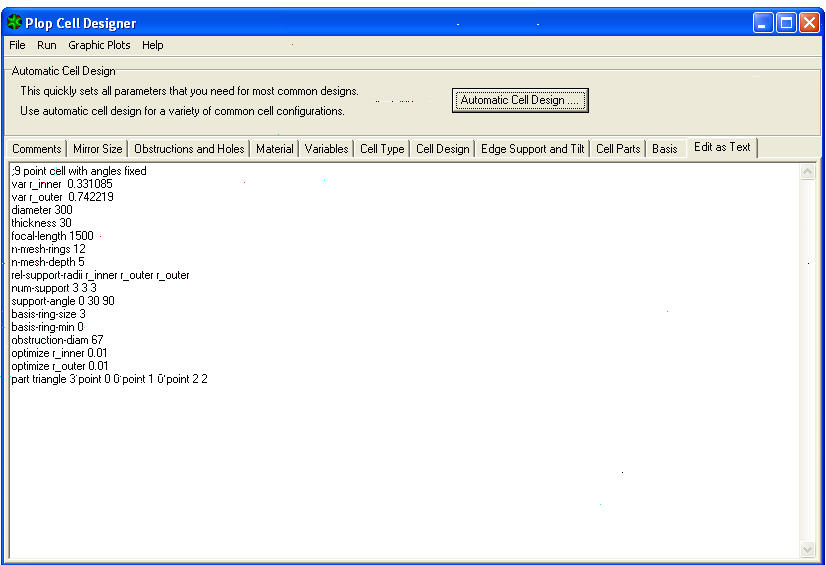
7) Préparez-vous à dessiner la cellule avec un CAD, ou autre méthode de dessin manuel:

8) Dessinez d'abord le cercle de diamètre du miroir primaire (300mm);

9) Il faut maintenant chercher, parmi les nombreuses lignes des colonnes relatives aux variables affichées, celui qui nous permettra de calculer le rayon du cercle d'appui interne, qui est le VAR R_INNER 0.331085 – puis multipliez le rayon du miroir par ce coefficient 0.331085 pour obtenir le rayon du cercle intérieur de la cellule sur laquelle demeureront les 3 points d'appui internes, de notre barillet à 9 points.

(150×0.331085=) 49.66mm = rayon du cercle des 3 appuy intérieurs

10) Dessiner cet cercle concentrique au diamètre du miroir.

11) Cherchez ensuite la variable du rayon externe VAR R_OUTER entre les mêmes lignes en colonnes 0.742219 – et multipliez le rayon du miroir par ce coefficient pour obtenir le rayon du cercle sur lequel il y a d'autres 6 points d'appui.

(150×0.742219=) 111.33mm = rayon du cercle des supports externes.

12) Tracer cet cercle concentrique àux precedents.

13) Aller au MENU’ de la fenetre PLOP CELL DESIGNER, et cliquez sur le command GRAPHIC PLOTS, puis cliquez sur CELL PARTS:

 

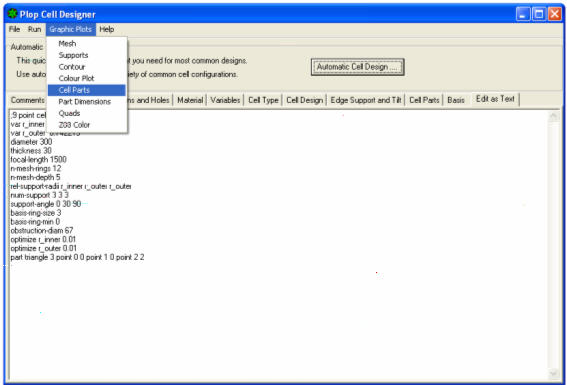
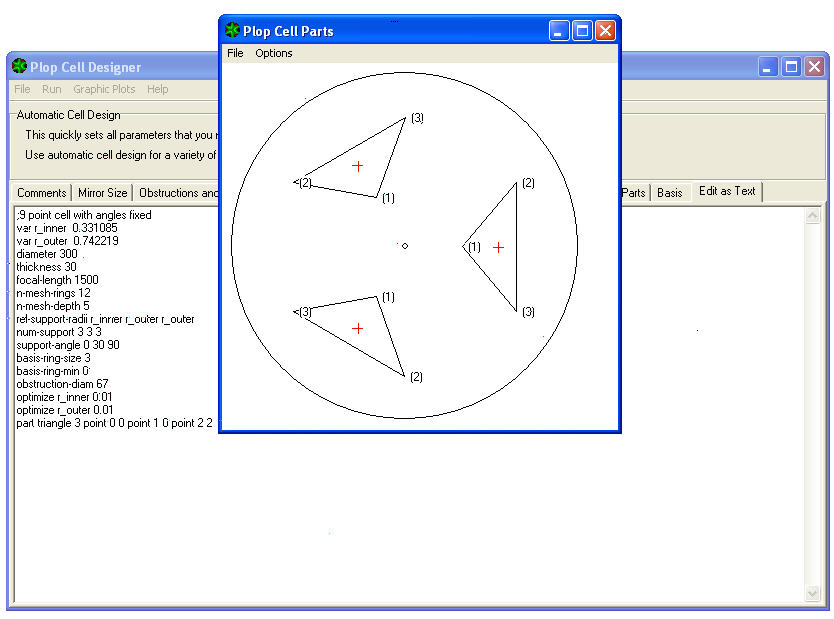
Vous verrez l’emplacement par rapport au miroir, des trois triangles isocèles de son support (car il a été choisi un barillet à 9 points qui offrent a l’appui les neuf vertex des trois triangles).

 14) À ce stade, fenêtre fermée PLOP CELL PART, nous sommes toujours sur la fenêtre ci-dessous qui affiche la liste des données déjà utilisées. Donc, pour continuer, nous devons d'abord fermer le fichier EDIT AS TEXT, en cliquant sur un autre classeur. Par exemple sur la BASE à proximité, afin d'éviter l'apparition d'une erreur de blocage “opération invalide en virgule flottante”l

Erreur est due à une incohérence entre le signe virgule, utilisé par Windows comme séparateur décimal en Italie, au lieu du point, Séparateur anglo-saxon requis dans les calculs du programme GUI PLOP.

ces calculs qu'il faut relancer sans plus les afficher, pour éviter l'erreur résultant du remplacement du séparateur décimal.

15) Dans la fenêtre PLOP CELL DESIGNER, nous cliquons sur le bouton AUTOMATIC CELL DESIGN, confirmer avec DONE les mêmes données précédemment introduites dans la carte RUN CONTROL en lançant START PLOP , et en appuyant sur OK une fois terminé

16) PLOP RUN CONTROL doit alors être fermé et renvoyé à la fenêtre PLOP CELL DESIGNER ci-dessous, dans le menu déroulant GRAPHIC PLOTS, choisissez PART DIMENSIONS.

  

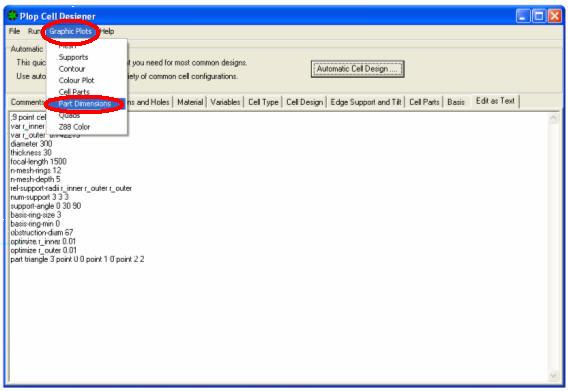
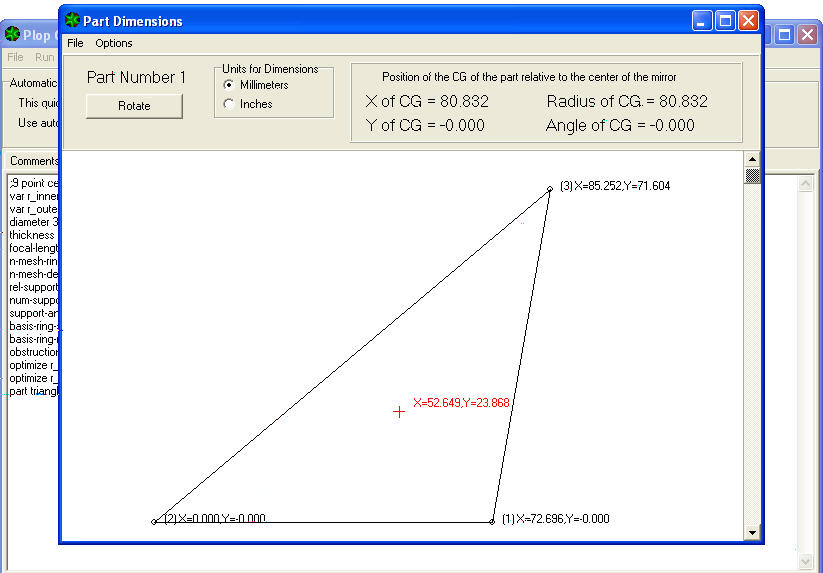
apparaît la fiche technique PART NUMBER 1, qui est l'un des trois triangles égaux, avec coordonnées cartésiennes des trois vertex de support, et du centre de gravité de chaque triangle,  qui va tomber sur une troisième circonférence encore à dessiner, et intermédiaire entre les deux déjà dessinè pour les points d’appui du miroir.

La boîte en haut et a droite indique la position du Centre de gravité (CG = Centre de gravité de la pièce affichée), donnéen coordonnées relatives par rapport au centre du miroir avec:

Coordonnée X du centre de gravité = 80.832mm et coordonnée Y = 0:

Ce qui signifie que le Centre de gravité est à la verticale (Y = 0) du centre miroir, à une distance (de rayon ) du centre de 80.832 mm (coord. Y):

Distance qui individue cet troisième cercle sur lequel résideront, a 120 degrés l'un de l’autre, les trois centres de gravité des trois triangles à l’appui du miroir.

17) Puis tracez donc le cercle concentrique de rayon 80.332 mm siège des support des trois triangles.

En regardant maintenant l'image du triangle afficher, Nous notons que, soit les vertex que le Centre de gravité sont indiqués en Coordonnées cartésiennes se référant cette fois au point 2 (vertex 2 en bas à gauche) du triangle, qui ait coordonnées X = 0 et Y = 0, indique que le « point zéro départ » des mesures suivantes.

le point 1 (la ligne droite horizontale inférieure) Il à donc coordonnée X = 72.696 et Y = 0, ce qui signifie que il est long comme son abscisse, vis a dir 72.696 mm, sans aucune variation d'ordonnèe (parce que Y = zéro).

18) Nous écrivons cette valeur pour ne pas l'oublier.

La fenêtre avec le triangle affiché, présente le bouton de fonction ROTATE, avec lequel vous pouvez faire pivoter le triangle dans le sens antihoraire, et faire apparaître a chacque pression, chacun de ses trois vertex (le premier sommet était le nombre 2; le second sera le # 3 et le troisième n. 1) dans le point – origine des coordonnées X = 0; Y = 0,  qui est à la gauche de l'image sur l'écran.

De cette façon, pour chaque rotation qui nous demanderont, nous verrons progressivement la longueur de chacque côté, couché horizontalement au bas, indiqué par son abscisse X.

19) Annottoms noius, même les deux valeurs restantes, qui avec le premier identifierons les dimensions de chacun des trois triangles. (Deux de ces trois valeurs seront identiques, parce que il s'agit des triangles isocèles).

20) Il ne reste qu’à dessiner les trois triangles à 120° de distance l'un de l'autre, en plaçant 6 points de 9 en totale, par rapport aux extrêmes de leurs hypoténuses, sur la circonférence de rayon extérieur (VAR = R_OUTER) 111.33mm;

Et vérifiez que les trois points relatifs à leurs HAUTEURS tomberont sur la circonférence de rayon INTERIEUR (VAR R_INNER =) 49.66mm.

Alors que leurs Centre de gravité se trouve sur la circonférence intermédiaire de rayon 80.832 mm

PRENEZ NOTE QUE: Dans cet exemple de simple barillet a 9 points, le "CELL PARTS" n'est qu'une seule, c'est-à-dire composé du triangle de support du miroir (dans ce cas à faire en trois exemplaires identiques).

Alors que si vous avez choisi un barillet avec 18 points, les "CELL PARTS" seraient deux: c'est-à-dire comme part 1 il y aura le triangle support miroir, (dans ce cas à réaliser dans 6 spécimens identiques) et comme part 2 la barre d'haltères qui supporte chacune des trois paires de triangles (à faire en trois exemplaires).

Et donc aussi pour d'autres cellules compliquées par de plus nombreux points d'appui, l'affichage des données relatives aux "CELL PARTS" supplémentaires est obtenu en poursuivant au-delà de l'affichage de l'élément numéro un (qui est généralement l'un des triangles de support du miroir), en faisant défiler avec le "mouse" le curseur à droite de la fenêtre qui affiche le triangle lui-même. Tout autre élément constructif apparaîtra, de la manière habituelle, montrant toutes les informations de sa position dans la case en haut, et au centre de la fenêtre ses dimensions, qui peut éventuellement se référer aux coordonnées cartésiennes de l'élément qui se trouve a la base du dessin, tournable sur soi meme comme décrit dans le cas du triangle dans ce tutoriel se référant à une cellule a 9 points, pour identifier de temps en temps les données relatives au côté qui est en position bas et horizontale.

FIN DU DESSIN DU BARILLET.

Si maintenant nous revenons au point 13) PLOP DESIGNER CELLULAIRE, Cliquons sur GRAPHIC PLOTS, Nous avons la possibilité de choisir de voir d'autres représentations graphiques du miroir et des déformations qui l'affligeront lorsqu'il serait monté dans la cellule conçue .

La première visualisation possible est obtenue en cliquant sur le menu déroulant TERRAINS MESH GRAPHIQUE, pour voir comment la surface du miroir est divisé dans le réseau de polygones de surface égale, identifié comme “éléments finis” Je suis pris en compte dans le calcul.

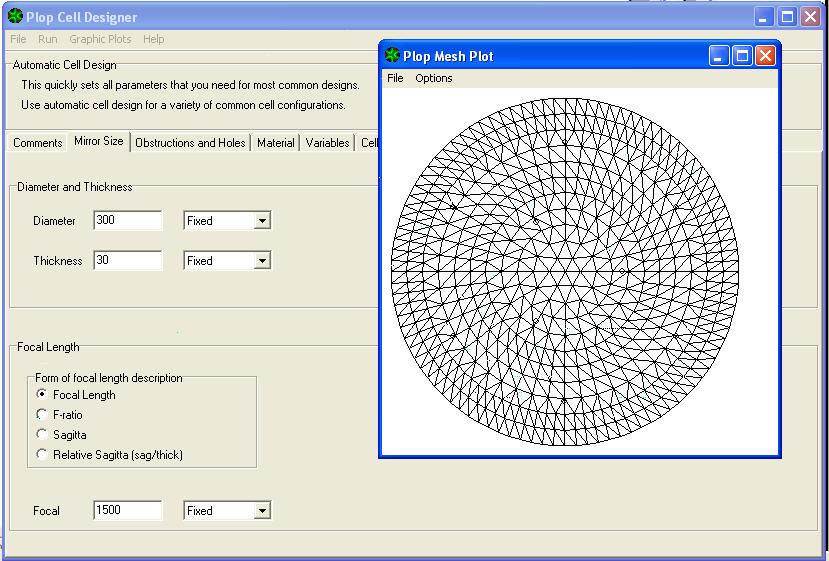
Le deuxième voix du menu est SUPPORTS, et nous L'avions déjà vu plus haut.

Le troisième voix du menu est le stress CONTOUR et montrera les lignes des stresses autour des points d’appui. Une sorte de lignes de contour, des lignes indiquant les changements de niveau homogènes (mais infinitésimale) atteinte par la surface déformée, même le stress.

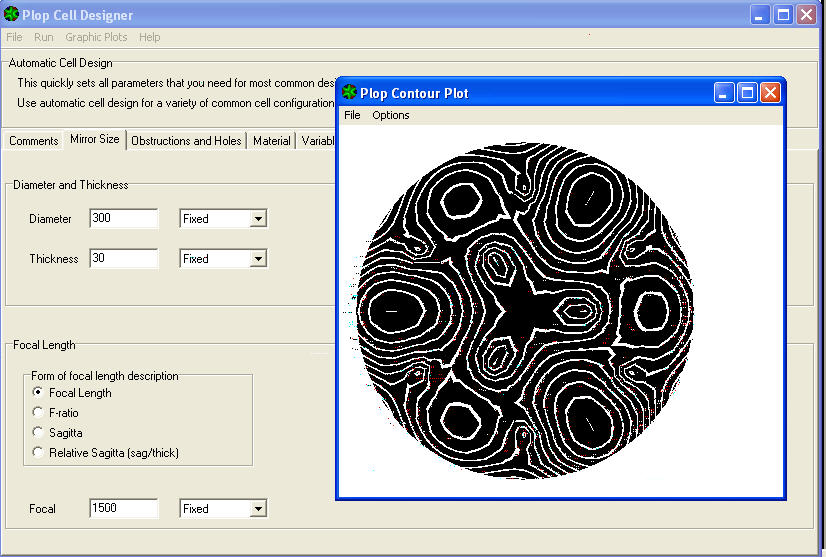
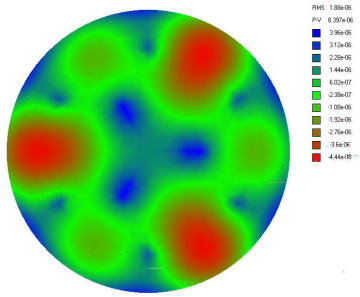
Le quatrième élément du menu est le COLOURPLOT intéressant qui va montrer une carte avec les quantitès des déformation exprimée soit en ce qui concerne RMS comme “rMS” relatif à toute la surface, QUEau niveau locale dans les diverses couleurs d’une échelle indiquè a côté, indiquant Valeurs de PIC/VALLEt les déformations générées.

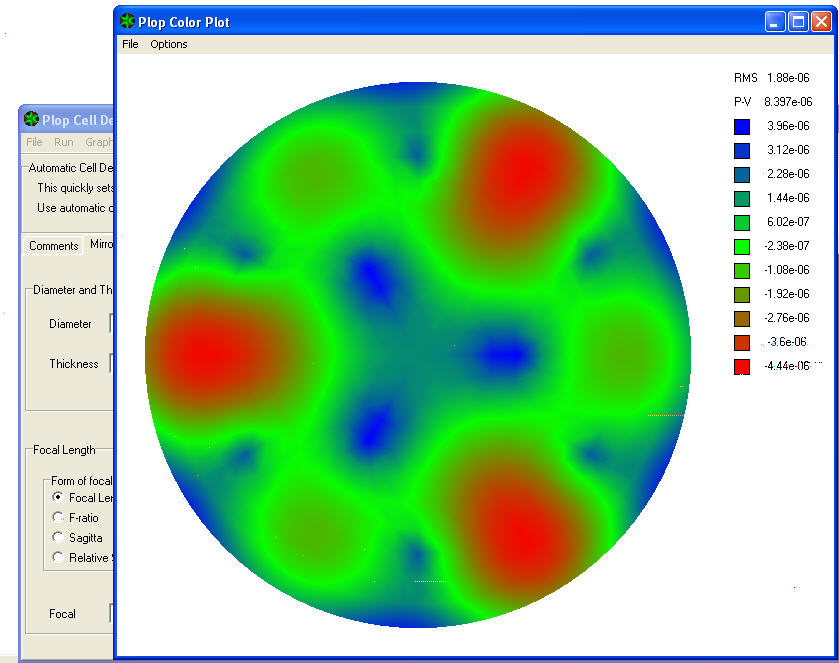
La valeur de RMS 1,88 Exponent-06 détectable dans la colonne plus en haut à droite du graphique, Il indique la valeur effective (ou de déviation quadratique moyenne ) de l’erreur produit sur toute la surface du miroir par ce type de barillet , par rapport à la longueur d’onde (lambda) de 550 nanmetres de la Lumière jaune-vert que l’oeil humain est plus sensible;

Alors que le sous-jacent P-V 8.397E-06 indique l'erreur exprimée en pic / vallée, ou bien minimale et maximale locaux de la surface .

Dans la pratique, les zones en couleur bleu sont les moins déformées car bien supportées par les points d'appuy du miroir; tandis que les espaces verts sont déformation intermédiaire, et les rouges sont les plus déformées.

Comment faire pour avoir une idée de la bonté de la cellule choisie?

Même sans recourir aux mathématiques pour une précise quantification technique , on lit le texte du guide du logiciel“PLOP USER. PDF”, la suggestion qu’une erreur RMS de 4.2 xponent-06 mm correspondant à un Lambda/128, est considéré comme une limite assez bonne pour une cellule-barillet.

Notre barillet donne dans la graphique une valeur RMS de 1,88 exponent-06, C'est a dire 2.23 fois plus petits, et donc d'autretant meilleur, la limite indiquée aussi bien raisonnable pour une cellule.

Maintenant que nous avons eu une idée de l'ampleur de la qualité de notre cellule, Nous procedons a voire a quoi servent les autres voix-éléments contenues dans le menu.

Nous continuons donc et et nous finissons par ignorer les cinquième et sixième voix cellule CELL PARTS et DIMENSIONS, que nous avons deja profondement vue plus haut, et nous rencontrons la dernière entrée “Z88” du menu déroulant, qu'il n'est pas de notre intérêt direct, car elle concerne l’utilisation d’une extension du logiciel, appelée Z88 pour “initiés” du calcul par éléments finis.