In the design phase of our astronomical mirror, it is essential to determine the focal length at which you want to reach, since the same focal length depends on the extent of the arrow, ie the depth of the center of the mirror with respect to its edges that we will achieve especially in the roughing phase. The formula for calculating the extent of the arrow is the following:
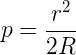
where p is the depth at the center mirror (said exactly arrow), r the mirror radius and R the radius of curvature of the mirror, which it is simply equal to twice the focal, which, then, It is inversely proportional to the extent of the arrow same.
During roughing the mirror, to control the arrow (and therefore also determine to which of mere excavation of the working point is) It is used to measure directly on the mirror the depth of the same, for example using a template, one sferometro, the thickness of which is known measuring or a feeler gauge. They are all systems that return a control on the arrow to the maximum of the order of hundredths of a millimeter, but that at this stage of processing are more than enough.
In the final stages of the mirror processing, instead, the surface of the same is so polished that, to check the correct focal, you can mount it directly on the telescope, which of course we know the focal: despite the lack of aluminizing, we will still be able to focus a bright object if precisely the focal point is correct.
In intermediate stages instead, substantially after verifying that the arrow is correct to the hundredth of a millimeter, or at least the tenth, we are not yet able to measure the precise focal mounting the mirror on the telescope (the surface is still too opaque to reflect an image that can be focused also at the right focal), born, on the other hand, we are content to continue the grinding step with finer grains without the certainty of having reached with a certain accuracy the focal desired and without the possibility to check that during the machining of the mirror does not undergo undesired variations.
Exists, then, a simple system with which we can measure the radius of curvature tentatively reached by our mirror and, then, dividing the same for two, the focal. To perform the measurement with this system we need a support for the mirror, holding it vertically (who will return shortly useful for the Ronchi test and / or Foucault), a fairly powerful point source of light, and a glossy white surface and……..a bit of water.
We lay on the side of the mirror on the support darkened room. At a distance approximately equal to the radius of curvature (we know through the measurement of the arrow), frontally to the mirror surface, fix to a support (of any kind) the source of light aimed toward the mirror and the glossy surface and white parallel to the mirror and so that the light source is on the same plane of the surface itself.
Now: we know that the reflected light mirror sulo (that is certainly now spherical) recompose your picture exactly to the curvature of the mirror, revealing, then, this measure, which yields, dividing by two, the focal. We light, then, the light, bathe with a little’ water the mirror so that it reflects light better and we make sure that the light invests full mirror and the reflection of the same light is projected on the white surface and polishes. By moving the support surface with light and in the longitudinal direction with respect to the mirror, taking care that the beam of light will continue to invest the mirror and the projection of light on our terms “screen”, we find the focus point of the reflected light. It will be like to focus on a star: with a few movements will be able to find with some precision the point at which the reflection of light on the screen, after being enlarged and blurred, It will focus on a point that will be clear, “On fire”.
We found the radius of curvature: to measure, simply stop the support and measure the distance between the light plane / screen and the plane of the mirror.
And that's it!