Et’ utile à ce stade, un rappel sur les techniques de traitement avec les outils à la sous-diamètre, en particulier sur la façon dont il est possible augmenter la courbure d'une ou plusieurs zones.
Rappelons ensuite le concept selon lequel au cours du dernier avec le sous-diamètre, les zones externes augmentent leur courbure tandis que ceux à l'intérieur de la diminution, ce qui est de dire que, pendant le passé générer un “sillon” sur la surface, où le secteur central de la zone usinée est plus profond que le reste de la surface non usiné.
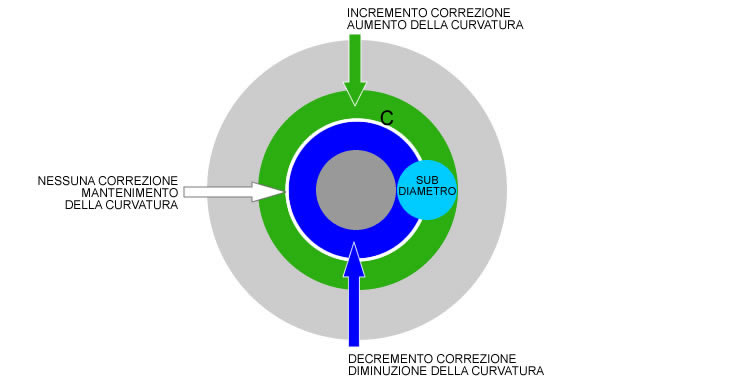
figue. 1 – Action sur le diamètre de la courbure sous-surface
théoriquement ( mais pas dans la pratique ) la seule application de cette technique est suffisante pour obtenir le résultat souhaité. nous voyons comment:
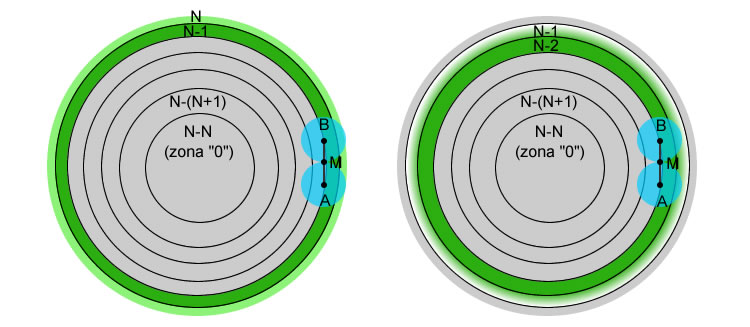
figue. 2 – Séquence de la courbure augmente dans les zones adjacentes.
assumer N comme le nombre total de zones qui divisent pratiquement notre miroir . Nous aurons donc notre succession de zones ( secteurs circulaires de largeur par défaut ) en partant du bord vers le miroir central: N, N-1, N-2, ….. , N-N.
Notre hypothèse de départ nous dit que la sphère et coïncident dans parabola le bord, mais étant donné que dans les tests que nous ne pourrons jamais avoir un moyen de mesurer la courbure du bord, rien ne nous empêche de “déplacer” Ce point de tangence ( Rappelez-vous que peut être choisie de manière arbitraire en tout point de départ de la section sphérique ) au centre de la zone la plus périphérique ( N ) , juste au moment où la mesure est effectuée.
Nous aurons donc que le centre de la dernière zone est par définition “correcte”, étant tangente à la fois la balle au profil parabolique du projet et ne doit donc pas être travaillé, alors nous commençons à excaver le centre de la zone suivante N-1 jusqu'à pas non plus être tangente au profil parabolique voulu.
Pour ce faire, nous devons faire de la région N-1 et son centre plus profond d'un des quartiers N par rapport à la sphère de départ, en d'autres termes, nous devons augmenter la courbure de passer de la balle initiale N-1 a N.
puis en appliquant le diamètre précité de la sous-technique, Nous préparons un outil dont le rayon est légèrement supérieure à la distance entre les centres des deux zones successives , Nous positionner le centre de l'outil sur le bord intérieur de la zone N-1 et effectuera des petits manèges çà et là avec un motif circulaire autour de la zone. Le résultat sera que nous aurons augmenté la courbure exactement entre la zone N-1 ed N. Nous ferons la mesure de cette augmentation avec un essai approprié, nous limiter à mesurer seulement “tirage” de ces deux zones, et nous réitérons sessions avec le sous-diamètre jusqu'à ce que le projet de mesure ne sera pas confondu avec celui de la simulation ( calculé mathématiquement ou par l'intermédiaire d'un logiciel ) de notre parabole finale .
À ce stade, nous avons deux zones correctes que la parabole de fin. alors nous allons passer à la zone suivante N-2 et répétez la même procédure “excavation” et la connexion entre la N-1 et N-2 jusqu'à amener ce tirage aussi à la valeur correcte.
Nous appliquerons la procédure successivement jusqu'à ce que la dernière zone N-N ( le centre du miroir ou “zone 0” ) veiller à ce que la dernière zone “utile” , la N-(N + 1) , qui est la première zone centrale , La configuration complète et la connexion de la parabole.
DANS LE “TROMPETTE DES TOLERANCES”
la génération de la parabole comme approfondissement croissant des zones consécutives, Il peut également être considérée comme une succession de zones d'écoulement “tolérance” dans le graphique Millies-Lacroix. Pour ce faire, nous devons recourir à un petit “maquillage” qui nous aidera dans la vue immédiate de ce que vous allez faire.
Notre sphère de départ avec des rayons de courbure identique des zones ( établir = 0 ) inséré dans le graphique ML d'un miroir hypothétique 300 mm F4 parabolique, Il aurait une représentation semblable à ce:
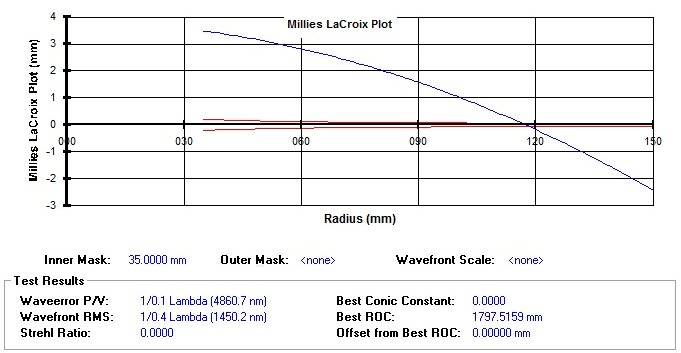
figue. 3 – Tableau Millies-Lacroix pour une surface sphérique ( l'échelle est modifiée pour une meilleure visualisation )
Appliquons maintenant notre première hypothèse, à savoir celle de tangence entre le bord de la sphère et parabole,( à la place du rayon 115 mm, comme illustré sur la figure) , qui est équivalent à traduire la courbe vers le haut jusqu'à la chute du centre de courbure de rayon 150 mm au centre de la trompette de tolérance:
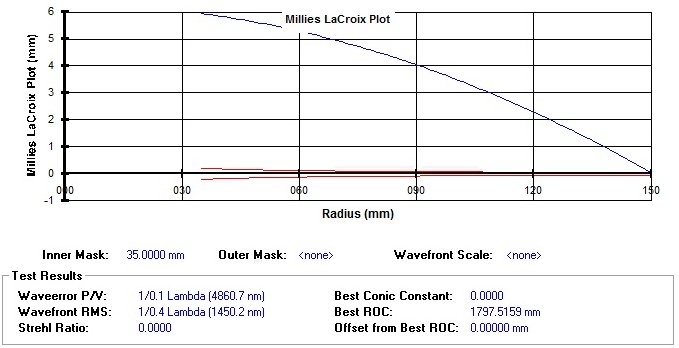
figue. 4 – Millies-Lacroix Graphique pour une tangente de la surface sphérique vers le bord avec le paraboloïde idéal ( l'échelle est modifiée pour une meilleure visualisation )
la traduction ( la “maquillage” ) nous venons de faire sur le match Ml graphique que nous avons choisi de le faire dans la section B de première partie de:
B - « Nous écourter » les réflexions centrales: Il revient à dire que, en partant du bord et nous passons progressivement vers le centre augmentera la courbure du miroir de telle sorte que les réflexions des zones centrales convergent plus, juste assez pour les faire coïncider avec les dispositifs.
En observant le graphique configuré de cette manière, est tout à fait intuitive, de mettre la balle à la parabole, toute la courbe sera en tolérance, Il faut donc approfondir la surface (“démolir” la courbe ) de plus en plus à partir du bord vers le centre
Supposons que nous avons calculé les valeurs exactes des centres de courbure de notre parabole idéale et travailler le miroir selon la procédure, amener le premier rayon de courbure exact de la zone N-1 ( dans cet exemple N = 5 ) puis tous les autres. Voici ce que nous devrions nous attendre dans le graphique ML calculé selon la essai de Foucault, -à-dire la séquence de la zone des corrections après zone :
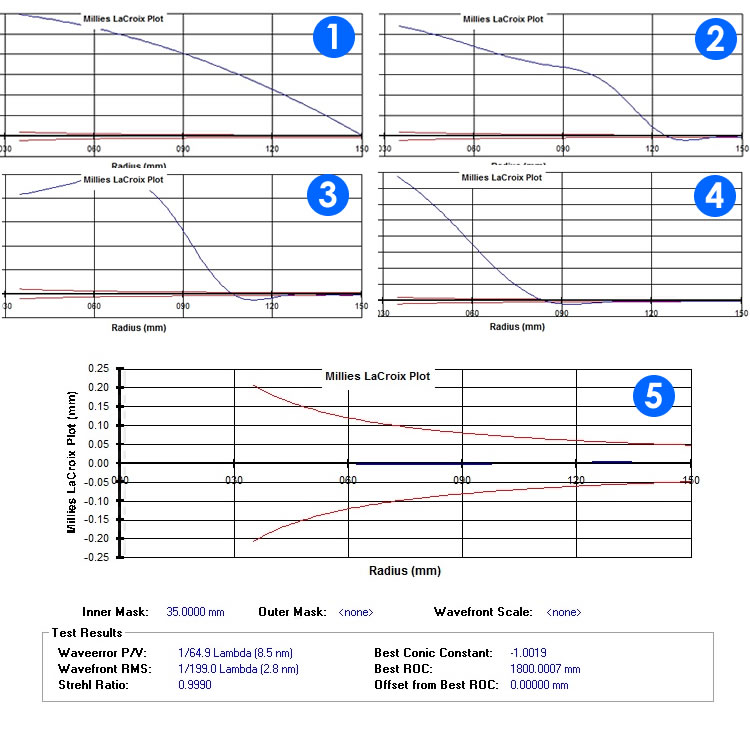
figue. 5 – Succession d'idées zonales.
Théorie à la pratique
comme mentionné, dans la pratique les choses ne sont pas la réalisation immédiate, Ils interviennent en fait différents éléments qui conseillent contre une telle approche directe, à trouver à l'avance des solutions à ces problèmes:
- pour les distances focales courtes, le nombre de zones à examiner doit être raisonnablement élevé, plus le nombre de zones est inférieure à l'extension de l'outil qui permet de ne travailler que deux zones adjacentes, sans interférer avec l'autre, deducible avec des incréments de temps de traitement.
- L'augmentation de la courbure de la surface externe diminue en conséquence celle de la zone intérieure qui sera ultérieurement approfondie tant en valeur par rapport à la sphère de la valeur supplémentaire de diminution de la courbure nouvellement générée.
- la partie inférieure de l'extension de l'outil, plus la probabilité de générer des erreurs de surface locales de correction difficile, les “petit” sous-diamètre doit être utilisé avec parcimonie , pour les petites corrections et une bonne expérience à utiliser dans moins configurations “extrême”.
- Il est difficile d'arriver à la mesure exacte du tirage au sort des deux zones agissant dans une seule direction, à savoir que l'augmentation de la courbure. Et’ probablement plus proche de la figure idéale dépassera ( bien que très peu ) dans le traitement et il est nécessaire de “revenir” -à-dire agissant dans le sens inverse pour diminuer la courbure, avec pour conséquence directe et inévitable de modification de forme aussi sur les zones adjacentes.
- Cette procédure ne permet pas une inspection complète de la surface lors de la construction de la figure, en particulier avec les tests complémentaires comme le Ronchi, Il est basé sur “confiance” que nous travaillons bien, mais la confirmation ne viendra que après avoir terminé toute la parabole.
Ce dernier point peut être mieux mis en évidence si nous simulons le graphique de test Ronchi correspondant à la zone de traitement après les phases de la zone:

figue. 6 – Simulation du test Ronchi pour l'approfondissement zonale de la relève.
Comme vous pouvez le voir sur la figure 6 , cette méthodologie tout en maintenant de bons locaux initiaux, Il ne permet pas d'évaluer immédiatement à quel point l'usinage sur les deux “droit stada”, qu'après avoir apporté toutes les zones personnalisées, nous évaluerons la correction de surface dans son intégralité.
Il est donc nécessaire d'optimiser cette stratégie dans tous les travaux de construction de la figure, pour rendre possible le contrôle de la qualité d'usinage pendant chaque phase, éliminer ou au moins réduire au minimum la possibilité d'erreurs locales ou générales et en permettant de les identifier avec certitude et d'intervenir “sans risque” si elle presentassero.
Et’ ce que nous découvrirons dans la troisième partie.