POUQUOI’ ÉTUDIER CE QUE LE LOGICIEL OFFRES NOUS DEJA’ PRÊT
L'étude des résultats du test de Foucault est très importante pour pouvoir évaluer indépendamment les conseils fournis par le logiciel préparé pour ce calcul. Personne est parfait et même des programmes pour ces calculs sont, alors qu'il est en mesure de mener également à l'objectif.
Comme alternatives pour arriver à ce but peut être beaucoup sinon infini, est intéressant d’utiliser notre propre sens critique correctement préparé, pour ne pas accepter aveuglément le verdict du logiciel.
Dans nos articles précédents, nous avons réalisé que pour faire un miroir parabolique l'on procede faisand des petits pas, n'etant pas techniquement possible de produire des parabolisations de la surface sphérique de verre d’un seul coup.
en article précédent nous avons vu comment se déroule le test de Foucault, sur la base de quelles évaluations de surface peuvent être calculées manuellement, afin de décider quelle retouche s’engagent dans la prochaine correction.
Voyons maintenant comment un programme informatique aurait élaboré les mêmes "tirages" détectés avec le test de Foucault et utilisés dans le calcul manuel du précédent article.
Comme logiciel Je me réfère donc aux parties d’une feuille excel de moi traduit et adapté, qui est disponible sous sa forme originale à l'adresse indiquée sur la même feuille.
Utilisez cette feuille de préférence, dû au fait que tout en m’offrant SA meilleure solution, Il me permet de simuler d'autres moyens personnels, et prédire les résultats. C'est ce que d'autres programmes de gestion du test Foucault plus rigides ne permettent pas avec la flexibilité d'une simple feuille de calcul.
Voyons voir:
UN CALCUL INFORMATIQUE DE L’ESSAI DE FOUCAULT
Nous trouvons dans la figure 1 qui ont été saisies dans la case E,F,g,H 27, les données suivantes de quatre tirages liés à 4 zones du miroir en examen
| 31.00 | 31.50 | 31.80 | 32.00 |
Nous savons déjà que pour vérifier les performances de la courbe parabolique brut que nous construisons, devrait « chevauchement » de référence de la parabole parfaite en mettant les deux courbes en contact direct, et même comparaison directe, en un point commun, qui peut être tout point « hm » notre courbe prise le long du rayon du miroir.
Cela nous permettra de voir, selon le « point de contact » choisi, quels sont les écarts tirés de notre courbe par rapport à la référence, pour déterminer quelle est la condition la plus favorable à une correction qui nous prend dans la poursuite des travaux, pour obtenir le plus près possible de la parabole de référence.
Ce chevauchement de la pratique des deux courbes simulent parfaitement avec les chiffres, au moyen de la soustraction pour tous les domaines de mesure, une constante appropriée (loin) ce qui conduit à la valeur zéro projet en un point pris comme contact mutuel.
Et la soustraction de cette même valeur à tous les domaines, simuler le chevauchement du mouvement de deux courbes, la qualité dont nous verrons un résultat immédiat des tableaux.
On se souvient alors que le mot « aberration » est un terme technique qui indique effectivement le degré de déformation que notre parabole il a à ce moment-là, par rapport à la sphère d'origine. (Ou bien doit avoir, si l'aberration est renvoyée à la parabole de référence).
L'aberration d'une zone, en d'autres termes, nous attirons mm EXPRIME la diversité que l'on trouve dans ce domaine parce que notre parabole est identique à la référence.
Et se souvenir encore plus, que le rayon de courbure R Il est un dérivé la distance focale réellement mesurée, qui est la base sur laquelle les aberrations de la parabole de référence sont calculés: Il devient crucial que la valeur de la distance focale est mesurée, vérifié et mis à jour dans la feuille de calcul, chaque fois que l'on suppose qu'il peut aussi être très peu changé après quelques réglages de correction impliquant le miroir central.
puis on calcule pour chaque zone, la « constante » de la distance qui séparerait les deux courbes, comme la différence entre nos rabattements (quelles sont les véritables aberrations de notre parabole en construction) avec des aberrations hm2/R. leur parabole de référence.
Nous soustrayons ensuite aux valeurs de la zone 1,2,3,4,
| 31.00 | 31.50 | 31.80 | 32.00 |
aberrations hm2/R. référence:
| 0.145 | 1.080 | 2.282 | 3.469 |
Et nous obtiendrons les possibles quatre constantes suivantes se chevauchent pour essayer un par un:
| 30.86 | 30.42 | 29.52 | 28.53 |
Donc, nous allons voir ce qui se passerait à notre courbe parabolique en construction, chevauchement de quatre façons différentes, une pour chaque zone, la parabole de blessure:
ZONE DE CONTACT 1
Si nous essayons maintenant de surimposer la constante 30.86 simulant le contact sur la première zone, l'insertion de la valeur 30.86 I28 dans la case « valeur considérée comme ». Les montre le tableau suivant qui les correctifs, et que les entités, devrait être fait dans les zones 2,3 e4, pour obtenir la parabole de référence.
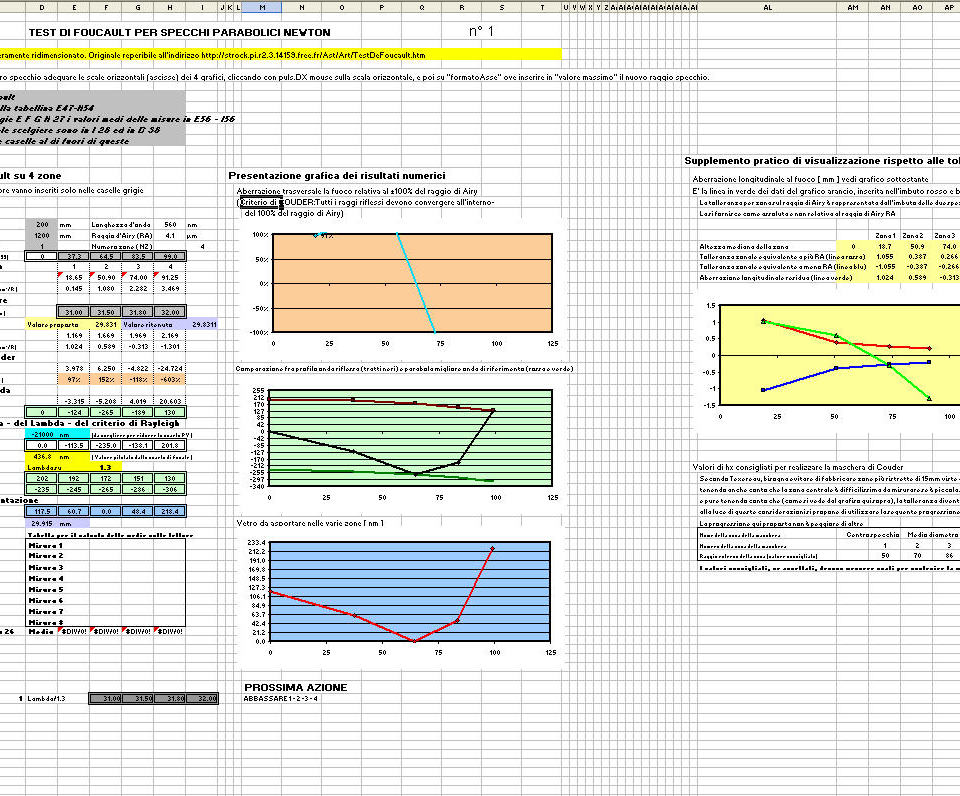
Aberrations relatives à la zone 1
Entretenez pour la région 1 (qui, en fait, il peut être vu parfaitement superposé à la faible parabole de couleur verte, qui exprime les rouges supérieurs de pointe de la distance - le défaut de la vallée maximale dans lambda / 0,5) Nous nous trouvons dans parabolizzare pour le bord: que nous serions dans des conditions très défavorables, d'avoir un avantage extrêmement élevé avec la nécessité d'éliminer presque 500 verre nanomètres zone 4 e 3, ce qui voudrait dire trop de travail.
Verre à enlever afin d'obtenir la parabole de référence, en tanand bonne la zone 1
ZONE DE CONTACT 2:
L'essai Let superposant dans la région 2, en utilisant la constante 30.42 dans la boîte I28. Les montre le tableau suivant qui les correctifs, et que les entités, devrait être fait dans les zones 1, 3 e 4 pour obtenir la parabole de référence.
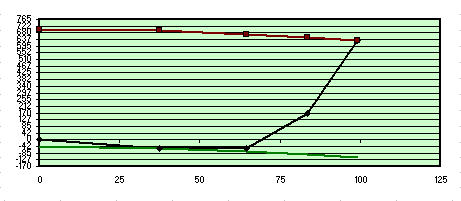
Aberrations relatives à la zone 2
Entretenez pour la région 2 (qui, en fait, il peut être vu parfaitement superposé à la faible parabole de couleur verte, qui exprime les rouges supérieurs de pointe de la distance - la vallée maximale de défaut contenue dans lambda / 0,8) nous serions encore en parabolizzare pour la frontière, puis dans des conditions défavorables, même un peu mieux de la précédente, tout comme la zone 1 de 21,2 nanomètres perfection légèrement plus élevé; mais nous aurions encore avoir les zones 3 e 4 très élevé, avec une quantité de verre à enlever environ 362 nanomètres de la surface totale 4 e 3. Cela signifierait trop de travail.
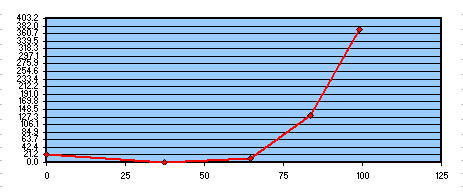
Verre à enlever afin d'obtenir la parabole de référence, en tanand bonne la zone 2
ZONE DE CONTACT 3:
L'essai Let superposant dans la région 3, en utilisant la constante 29.52 dans la boîte I28
Les montre le tableau suivant qui les correctifs, et que les entités, devrait être fait dans les zones 1, 2 e 4 pour obtenir la parabole de référence.
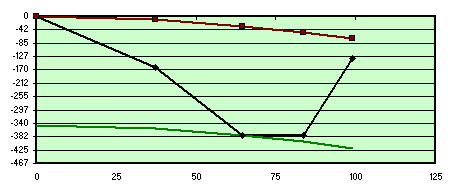
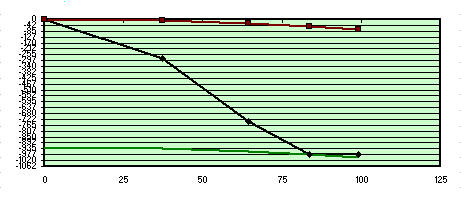
Aberrations relatives à la zone 3
Entretenez pour la région 3 (qui, en fait, il peut être vu superposé à la faible parabole de couleur verte, qui exprime les rouges supérieurs de pointe de la distance - le défaut de la vallée maximale dans lambda / 1,6) nous serions parabolizzare pour 70% du diamètre; nous serions en bon état, parce que nous aurions des zones 1 e 2 e 4 totale « High », mais facile à « réduire » . quand aucun risque, avec une attention particulière à la zone 4 pour éviter de travailler trop et mal, et obtenir à partir d'un bord agréable détecté un mauvais bord rétorqua impossible de corriger sans retourner vers le ballon.
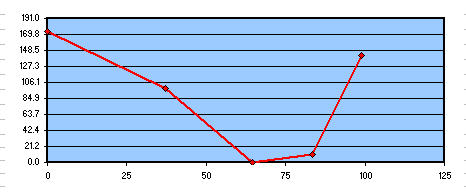
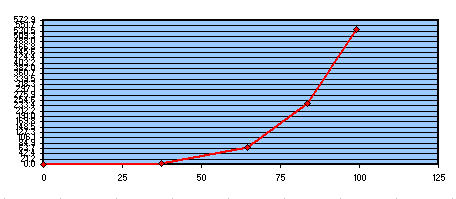
Verre à enlever afin d'obtenir la parabole de référence, en tanand bonne la zone 3
ZONE DE CONTACT 4:
L'essai Let superposant dans la région 4, en utilisant la constante 28.53 dans la boîte I28
Les montre le tableau suivant qui les correctifs, et que les entités, devrait être fait dans les zones 1, 2 e 3 pour obtenir la parabole de référence.
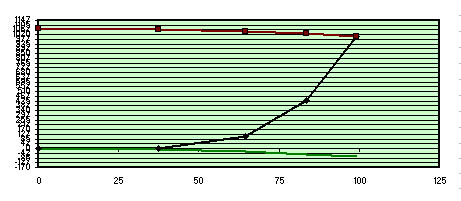
Entretenez pour la région 4 (qui, en fait, il peut être vu superposé à la faible parabole de couleur verte, qui exprime les rouges supérieurs de pointe de la distance - le défaut de la vallée maximale dans lambda / 0,6) nous nous trouverons a paraboliser pour le centre miroir, c'est-à-dire que nous nous trouverions à devoir choisir entre deux cas intéressants:
- la “mauvois” état de la zone centrale du miroir, donné par le fait que nous aurions les zones 1,2 e 3, a bien creuser 462 nanomètres, qui, ce ne serait pas pratique compte tenu du temps de travail plus long que nous aurions à faire, bien qu'avec de grandes tolérances d'usinage .
- la “excellente” condition de cette zone 4 du bord du miroir déjà parfaite, où les tolérances d'usinage sont très serrées. Excellent et tentant car, ce long travail d'abaissement des zones 1,2,3 centraòes bien éloignés du bord du miroir et avec une tolérance d'usinage très large, il se ferait loin du bord du miroir et sans aucun risque de bord rabattus.
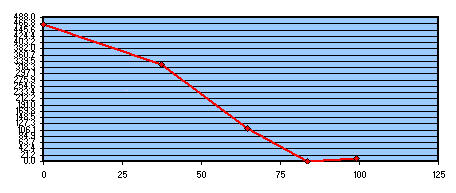
Verre à enlever afin d'obtenir la parabole de référence, en tanand bonne la zone 4
Ces quatre superpositions différentes, Je suis un exemple de la variabilité des travaux nécessaires en prenant comme points différents de référence, pour plus de simplicité, nous avons considéré le centre de nos quatre domaines.
POINT DANS LA SUGGESTION DU LOGICIEL ILLUSTRÉ 1:
En dépit de nos variations, les formules contenues dans le produit de feuille sera automatiquement une 29.831mm variables, le résultat de la somme de nos quatre mesures auxquelles la somme des quatre aberrations de référence a été soustrait, Enfin la médiation de ce résultat en le divisant par 4 comme il y a des zones, avec le résultat graphique suivant:
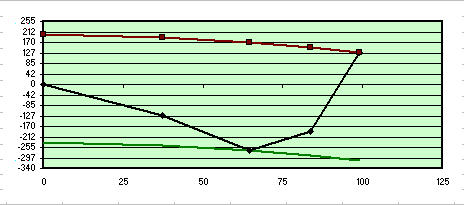
Aberrations relatives à l'espace calculées à partir de la feuille
Entretenez logiciel constant 29.83, qui indique un point situé entre la zone 2 il est à 3, (qui en fait, vous voyez ce point superposé à la faible parabole de couleur verte, que les exprime supérieurs rouges du pic à distance - le défaut de la vallée maximale dans lambda / 1,3) nous serions à peu près la parabolizzare 70% diamètre, que nous serions en bon état, bien qu'un 0.3 pire que ceux de notre simulation sur la zone de contact 3. Mais à ce stade du processus sensiblement équivalent à ceux de notre simulation sur la zone de contact 3, parce que nous aurions des zones 1 e 2 totale « High », mais facile à « réduire » , une zone 4 plus élevé que notre simulation, et le temps sans risque.
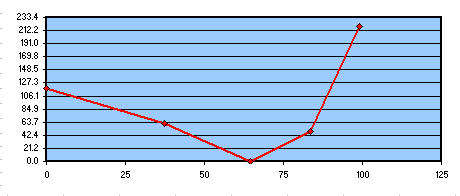
Verre à enlever pour obtenir la tenue référence parabole bon point de contact proposé par la feuille
QU'EST-CE QUE L'ON VEUT DEMONSTRER AVEC TOUT CE LA?
L'apparente futilité de ce raisonnement académique permet de vous familiariser avec les façons infinies qui mènent à un miroir parfait de parabolisation, dont le résultat ne dépend que de la persévérance de ceux qui travaillent, et d'avoir compris que derrière les résultats rigides et confortables fournies par le logiciel préparé pour le test Foucault, et du ne prendre et subir acritiquement ces résultats sans discernement.
En simulant manuellement il peut arriver qu'une rue soit trouvée “encore mieux que le meilleure”, pour obtenir un bon résultat impensable sans conditions de simulation.
la simulation est puissante et ne doit pas se limiter uniquement aux possibilités et aux dates des zones indiquées dans cet article, mais il peut être très utile en particulier pour essayer de changer les valeurs des tirages dans une ou plusieurs zones, de manière cohérente et probable avec la prochaine mesures correctives que nous avons déjà décidé d'entreprendre, de juger par nous-mêmes si cela que se passerait-il, est bon, et comme il est.
En fait, il arrive qu'en pratiquant les simulations on se rende compte qu'avec une légère action il pourrait obtenir surprise d'un lambda à deux chiffres, autrement inimaginable.