I TEST AMATORIALI
La necessità di eseguire i test sulle ottiche in lavorazione, in genere con superficie riflettente parabolica per telescopi newtoniani, è finalizzata a poter constatare con essi la presenza di eventuali errori di forma della superficie del relativo specchio, e di tali errori ottenere le QUANTITA’, al fine di poter studiare ed applicare azioni di correzione per giungere ad avere una perfetta parabola (nel caso del telescopio newtoniano) o altra perfetta forma necessaria.
I test più frequentemente usati a livello amatoriale per la valutazione della figura della parabola in un obiettivo a specchio newtoniano per telescopi precauzionalmente con rapporto focale non inferiore a F4, ( che comporta una profonda curvatura della superficie riflettente per la quale è adeguato il test della Caustica) sono due: Il test di RONCHI e il test di FOUCAULT.
Si tratta di due test COMPLEMENTARI fra loro, in quanto:
- IL TEST DI RONCHI:
Avviene guardando un reticolo di un certo numero di linee parallele per millimetro, riflesso dallo specchio in esame. Una superficie omogenea presenterà l’andamento di tali linee altrettanto omogeneo, cioè senza repentine variazioni di direzione localizzate in punti che sono da ritenersi difettosi. Ecco il motivo per cui esso mostra solo visualmente la qualità di TUTTA LA SUPERFICIE dello specchio (cosa che invece il test di Foucault non può fare), e quindi permette di individuare DOVE si trovano su di essa gli eventuali difetti, ma non può specificare di quanto essi siano fuori della tolleranza prevista. Per questo motivo il Ronchi è considerato un test di tipo QUALITATIVO.
Mentre,
- IL TEST DI FOUCAULT:
Tecnicamente compie un confronto fra le misure (dell’ordine dei nanometri), della parabola teorica presa come riferimento costruttivo, con quelle della stessa posizione presenti sullo specchio che stiamo realizzando. In altre parole, ricordando che una parabola presenta dei raggi di curvatuta della sua superficie progressivamente maggiori man mano che si procede dal centro verso il bordo dello specchio, con il test di Foucault si cercano i centri di curvatura (e quindi i raggi) di ciascuna zona (cioè corona circolare in cui è sato diviso lo specchio dalla sovrapposizione di una maschera di Couder, a finestre) e si determinano gli scostamenti rispetto ai valori teorici che avremmo dovuto trovare in quella zona per avere una parabola perfetta.
Un valore rilevato più alto del dovuto indicherà la necessità di scavare ulteriormente, mentre uno più basso del dovuto suggerirà di scavare tutto il resto della supeficie tornando un poco verso la sfera, visto che il vetro non si può aggiungere dove già è mancante.
La grande potenza del test di Foucault è inoltre data dal fatto che si può simulare il contatto fra le due parabole, quella teorica e quella pratica, in qualsiasi loro punto, per visualizzare graficamente e quantitativamente in nanometri da asportare, se gli scostamenti del resto della parabola sono convenienti per la lavorazione, che, viste le tolleranze in gioco, è notoriamente più facile al centro che non al bordo dello specchio.
In pratica quindi il test di Foucault misura in modo molto preciso la qualità sulle zone di UN DIAMETRO della superficie riflettente, fornendo le QUANTITA’ degli errori eventualmente presenti su di essa. Cosa che il Ronchi non può fare. Per questo motivo il Foucault è considerato un test di tipo QUANTITATIVO.
Il fatto che la misura del Foucault avvenga su un solo diametro e non su tutta la superficie dello specchio in esame, non ne diminuisce l’efficacia, poiché la tecnica di lavorazione per ricavare la curva scavata nel vetro dello specchio, è fatta di migliaia di passate abrasive “avanti e indietro”, di un utensile di pari diametro dello specchio o poco minore, contemporaneamente fatto ruotare in modo tale da costruire quello scavo come viene costruita una classica figura di rivoluzione.
Quella figura di rivoluzione così costruita è in grado di garantire che: SE in una determinata posizione del diametro in esame sono presenti difetti, essi saranno presenti in medesima quantità sulla intera corona circolare comprendente quella determinata posizione.
Viceversa, se i difetti non saranno presenti su quel diametro, non lo saranno nemmeno sulla corona circolare che comprende quella posizione.
La garanzia di cui sopra è data sia dalla grande dimensione dell’utensile che dal comportamento dell’operatore:
Dall’utensile: Che per questo lavoro iniziale di realizzazione di uno scavo, non deve essere di piccolo diametro, il quale non scaverebbe in modo uniforme su tutta la superficie.
Dal comportamento dell’operatore: Che si mantiene entro i semplici limiti della buona tecnica specificata da alcuni generi di corse (strokes in inglese), da applicare con l’utensile sullo specchio, oppure con lo specchio sull’utensile, per abradere più il centro non toccando il bordo, o viceversa più la periferia non toccando il centro, od ancora di alternarli per mantenere la curvatura raggiunta.
Buona e semplice tecnica che in sostanza impedisce a chi la mette in pratica di commettere errori importanti all’interno delle zone che costituiscono uno specchio, e quindi porta automaticamente a realizzare uno scavo sferoide, dal quale sarà molto più facile realizzare la ulteriore leggerissima svasatura verso il bordo, cioè la parabolizzazione, per conferire allo specchio la forma parabilica desiderata.
Parabolizzazione che per specchi realizzati con un rapporto focale maggiore di F6, non è nemmeno necessaria, essendo lo scavo della parabola talmente poco profondo da confondersi con la sfera originata dal lavoro iniziale.
Per questi motivi la valutazione col Foucault di un solo diametro, è potenzialmente estensibile alla intera superficie. Ma è bene non privarsi della soddisfazione di una verifica eseguita col test di Ronchi.
JEAN BERNARD LEON FOUCAULT
Grande fisico francese, fu il primo a usare il vetro per la fabbricazione di specchi per telescopi in sostituzione del metallo usato in precedenza.
Fra le sue invenzioni c’è infatti nel 1858 il metodo di realizzazione per rivoluzione degli specchi parabolici in vetro per telescopi, ed anche il metodo geniale e semplicissimo per misurare manualmente la distanza focale di una superficie riflettente curva, con una precisione che potrebbe sembrare impossibile non solo per quei tempi ma anche attualmente.
- IL SUO METODO DI REALIZZAZIONE DEGLI SPECCHI PARABOLICI prevede l’utilizzo di due dischi di vetro, dei quali uno sarà il futuro specchio e l’altro l’utensile.
Lo scavo della curva che risulterà sferica, si esegue posando il disco di vetro utensile su un tavolo rotondo, e strofinando lungo il suo bordo il centro del disco che diverrà lo specchio (con interposizione di abrasivo in polvere, acqua, e contemporanea rotazione dell’operatore attorno al tavolo)
LA FORMA SFERICA
Il risultato dell’abrasione protratta per molte ore, ed affinata con grane abrasive sempre più fini, darà al disco che si tiene in mano la forma CONCAVA sferica dello specchio (questo perchè lo abbiamo prodotto strofinando il suo CENTRO contro il BORDO dell’utensile), e al disco dell’ tensile posto sul tavolo, darà la forma complementare sferica CONVESSA (ovviamente perchè nell’abrasione si è consumato il suo bordo).
La forma riflettente sferica però sappiamo non essere in grado di focalizzare i raggi provenienti dall’infinito per formare una immagine in un solo punto. Questo avviene perché possedendo la forma sferica un unico raggio di curvatura, farà convergere i raggi che colpiscono lo specchio in periferia, in punti dell’asse ottico distanti dal luogo dove convergeranno quelli che colpiscono lo specchio al centro, e il risultato di tutto ciò sarà una macchia sfocata illeggibile.
LA FORMA PARABOLICA
Pertanto per realizzare un telescopio riflettore occorrerà “parabolizzare”, cioè svasare progressivamente dal centro al bordo la sfera originaria, portandola alla forma parabolica, aumentando cioè in modo progressivo e continuo, via via dal centro verso la periferia dello specchio, il raggio di curvatura della superficie riflettente.
DIFFERENZA FRA FUOCO E CENTRO DI CURVATURA DI UNA SUPERFICIE OTTICA
Il termine “fuoco” è utilizzato in ottica per indicare il luogo di formazione di una immagine, mentre il centro di curvatura di una superficie, è in un certo senso il precursore geometrico del fuoco, perchè si trova al doppio della distanza focale, ed è utilizzato nella lavorazione.
PERCHE’ IN LAVORAZIONE SI USA IL CENTRO DI CURVATURA ANZICHE’ L’OMOLOGO FUOCO
E’ noto che uno specchio parabolico riceve la luce delle stelle proveniente dall’infinito, e la concentra in un punto di “fuoco”, posto appunto alla lunghezza focale di tale specchio, che come già anticipato, geometricamente vale la metà del raggio di curvatura di ogni sua zona riflettente.
Nella fabbricazione di uno specchio vi è la ovvia esigenza di misurare moltissime volte la curvatura progressiva della superficie parabolica per far si che la parabola realizzata venga ripetutamente corretta fino a che essa sia la più perfetta possibile.
Ma per così tanto e preciso lavoro, sarebbe contrario ad ogni praticità utilizzare una stella posta all’infinito per realizzare tali ripetute misure in laboratorio (anche se tale “star test” è molto utile e lo si fa regolarmente “una tantum” sul campo delle osservazioni per verificare la corretta collimazione delle ottiche).
In fase di lavorazione Leon Foucault quindi utilizzò una sorgente luminosa puntiforme ad illuminare lo specchio, non posta “all’infinito”, ma posta molto più comodamente sul suo banco di lavoro, e scoperse che ponendo un occhio a captare il riflesso dello specchio lateralmente, ma molto vicino al fianco della sorgente ed “a cavallo” del centro di curvatura, era in grado di vedere tale specchio completamente illuminato nonostante la sorgente fosse puntiforme, ed inoltre, intercettando i cono di luce riflesso con la lama di un coltello, era in grado di vederne il progredire dell’ombra , e dal senso di progressione, era in grano di identificare la esatta posizione del centro di curvatura di ogni zona il lavorazione.
Aveva in sostanza trovato un metodo altrettanto valido di verifica della lavorazione utilizzando la distanza del centro di curvatura che diviene accessibile se si usa una illuminazione posta “quasi” nel centro di curvatura, invece di utilizzare il fuoco dello specchio, che avrebbe richiesto la sorgente posta ad uno scomodissimo infinito.
Tutte queste parole per dire che la differenza di usare la sorgente “quasi” al centro di curvatura comporta che può sfuggire nelle descrizioni pratiche di indicare con la parola “fuoco” quello che in realtà ne è il suo precursore, cioè il centro di curvatura della zona dello specchio; oppure di indicare impropriamente come posizioni “intrafocali” od “extrafocali” le loro omologhe posizioni precorritrici di inserimento della lama nel test di Foucault in posizioni rispettivamente “prima”e “dopo” il centro di curvatura.
Se ciò avviene si tratta di una imprecisione che dal punto di vista pratico è di poco conto, sapendo che si tratta di posizioni sostanzialmente omologhe.
Un ultima precisazione: L’uso dell’avverbio “quasi” ad indicare la posizione nel test di Foucault dell’occhio dell’osservatore e della sorgente, simmetricamente molto vicini al centro di curvatura, è indispensabile perchè il porre la sorgente nell’esatto centro rifletterebbe l’immagine su se stessa, e non sarebbe visibile dall’operatore.
Da qui la pratica necessità di spostare la sorgente di “poco” a sinistra e “quasi” nel centro, in modo che l’occhio di poco a destra possa vedere le ombre altrimenti inaccessibili, e quel “poco”, nella realizzzione di specchi con rapporto focale uguale o maggiore di F5, non è di solito in grado di creare astigmatismo, che al contrario potrebbe creare un disassamento maggiore.
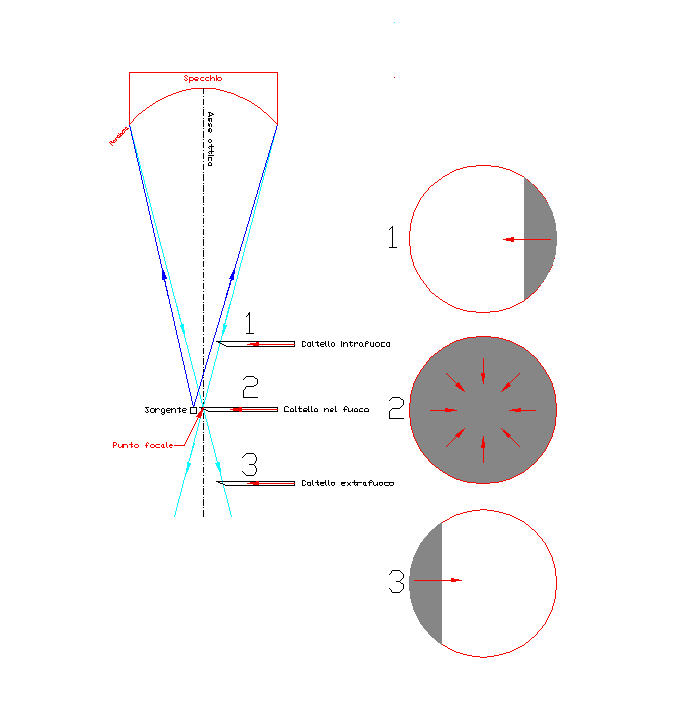
IL METODO DI FOUCAULT PER LA MISURA DEI RAGGI DI CURVATURA delle superfici, è geniale nella sua semplicità, e diviene comprensibile facendo riferimento al seguente disegno (fare clic per ingrandire):
Il principio è quello di porsi con gli occhi vicino al centro di curvatura dello specchio sferico (vedi disegno), di fronte al centro dello specchio sistemato su un supporto con l’esse ottico di riflessione orizzontale, e di puntare verso il suo centro una sorgente luminosa puntiforme (vedi nota*) posta anch’essa di fronte all’incirca al centro specchio, e sul fianco sinistro dell’occhio dell’osservatore.
(*Nota DIMENSIONI OTTIMALI DEL FORO STENOPEICO, O DELLA PIU’ COMODA FENDITURA: Per un buon risultato pratico del test di Foucault, Jean Texereau, a pagina 60 del suo libro “La construction du telescope d’amateur”, suggerisce che il diametro del foro stenopeico, oppure la larghezza della fenditura, siano compresi fra i 20 e i 50 micron.
Ricordando che (per esempio) in una macchina fotografica, la chiusura del diaframma aumenta la profondità di campo e la nitidezza della immagine, ma riduce la quantità di luce e richiede un tempo di posa più lunga; ne consegue che per quanto riguarda un foro stenopieco o una fenditura, si hanno gli stessi vantaggi.
Una larghezza inferiore della fenditura o del foro stenopeico, aumenterebbe certamente la sensibilità del test fino ad un massimo, raggiungibile quando essa fosse pari al diametro della tacca di diffrazione dello specchio in corso di realizzazione.
Ma una fenditura così stretta (o un foro stenopeico così piccolo), genererebbero però una grande quantità di fastidiose frange di diffrazione che renderebbero molto più difficile la valutazione delle ombre (a meno di provare a utilizzare un web-cam per guardare l’andamento delle ombre su un monitor).
In realtà una sorgente puntiforme, o foro stenopeico di diametro 10 oppure 20 micron, non avrebbe la intensità luminosa sufficiente a svolgere bene il test, e quindi si utilizza in sua vece una fenditura verticale, la quale avendo larghezza pari al diametro del foro desiderato (cioè fra i 20 e i 50 micron) ma essendo estesa in altezza per circa 4 o 5 mm, fornisce le stesse caratteristiche diffrattorie del foro stenopeico, ma è molto più luminosa di esso e molto più facile da costruire (… avvicinando due lamette con interposto un pezzo di sottilissimo nastro magnetico da compact cassette che funziona da distanziale, e va tolto quando le due lame siano fissate con nastro biadesivo).
Fine della nota sulle dimensioni della fenditura o del foro stenopeico).
L’osservatore cercherà di muovere la sorgente a il suo occhio finchè non vedrà lo specchio completamente illuminato. Cosa che avviene quando la distanza dell’occhio e della sorgente è vicina al raggio di curvatura della zona centrale dello specchio (raggio di curvatura che è il doppio della lunghezza focale).
IL CONO DI LUCE RIFLESSA
In quella configurazione si genera un CONO DI LUCE (linee di colore azzurro nel disegno) che dalla curvatura della superficie dello specchio viene riflessa verso l’osservatore.
Il cono che ha come base il diametro dello specchio, ha come vertice il centro di curvatura, cioè il punto sull’ asse ottico che parte dal centro dello specchio, in cui tutti i raggi convergono e si incrociano.
Osserviamo però che OLTRE il punto di centro della curvatura, i lati del cono di luce continuano verso l’operatore incrociati, vediamo cioè i raggi di luce provenienti dal lato sinistro del cono, che proseguono la loro corsa sul lato destro, e viceversa i raggi destri proseguono sul lato sinistro.
LE OMBRE PRODOTTE DA UNA LAMA INTRODOTTA NEL CONO:
Se ora l’osservatore, vedendo lo specchio completamente illuminato, introduce nella luce riflessa una lama verticale, con movimento da destra verso sinistra* (vedi nota tecnica più avanti), potrà vedere l’ombra di quella lama in tre modi diversi, a seconda che essa sia stata introdotta prima del centro di cutvatura (in posizione “intrafocale” 1 nel disegno) ; oppure oltre il centro (in posizione extrafocale 3 nel disegno); oppure nell’esatto centro (posizione 2 del disegno).
POSIZIONE “INTRAFUOCO”
Supponendo che l’osservatore veda la lama come nel disco 1 di figura provenire da destra verso sinistra (cioè concordemente al verso della sua introduzione nel cono di luce), guardando il disegno comprenderemo che la provenienza da destra dell’ombra è data dall’intercettare della lama i raggi sul lato destro del cono. Cosa che avviene solo in posizione prima del centro di curvatura.
POSIZIONE “EXTRAFUOCO”
Supponendo ora che l’osservatore veda la lama come nel disco 3 di figura provenire in senso contrario, cuiè da sinistra verso destra, guardando il disegno comprenderemo che la lama (che sta fisicamente sempre sulla destra) mostra quella ombra quando intercetta i raggi dopo che essi si sono incrociati nel centro di curvatura. Quindi quando si è in posizione “extrafocale”.
POSIZIONE AL CENTRO DI CURVATURA
Quando invece l’operatore introducesse la lama nella esatta posizione del centro di curvatura, vedrebbe la superficie riflettente scurirsi in un grigio uniforme detto “tinta piatta” come in figura 2 del disegno, senza poterne apprezzare la progressione né da destra verso sinistra, né viceversa, ma vedrebbe l’intera zona scurirsi in modo ben diverso, come in seguito alla chiusura di un diaframma circolare.
A questo punto diventa chiaro capire come questo metodo permise a FOUCAULT di trovare la posizione dell’esatto centro di curvatura di qualsiasi curva semplicemente tastando l’introduzione della lama più o meno avanti sull’asse ottico dello specchio in esame.
(NOTA TECNICA*: Nella costruzione del semplice tester per eseguire il test di Foucault, non è obbligatorio ma è consigliabile attuare le n.2 seguenti regole “STANDARD” di uniformità generale:
- Movimento da destra verso sinistra della lama ortogonale all’asse ottico, per la sua introduzione nel cono di luce riflessa dallo specchio.
- Montaggio del micrometro a “verniero positivo” (cioè in modo che all’allontanamento corrisponda un aumento delle letture di misura degli spostamenti longitudinali avanti e indietro sull’asse ottico dello specchio in esame, denominati in gergo tecnico “tiraggi”).
FINE DELLA NOTA).
LA MISURAZIONE DEI RAGGI DI CURVATURA DELLA SUPERFICIE PARABOLICA
Non essendo possibile misurare in un solo colpo una curva con raggi continuamente variabili, è chiaro che occorrerà aggirare l’ostacolo suddividendo in modo fittizio lo specchio in una serie di corone circolari dette “zone”, non molto estese, in modo che all’interno delle quali il raggio di curvatura cambi in modo trascurabile, e pertanto possa essere considerato “comune”, trovando la “tinta piatta” della posizione di fuoco.
Posizione che, come abbiamo già detto, è sempre raggiungibile spostando opportunamente avanti o indietro il carrello del tester che porta la lama (a seconda che l’ombra sia vista rispettivamente provenire da sinistra o da destra), e annotando le letture dei “Tiraggi”, cioè dei millimetri di spostamento longitudinale lungo l’asse ottico dello specchio (con la precisione del decimo di mm o meglio del centesimo) corrispondenti alla posizione di centro di curvatura di ogni zona.
Tiraggi che sottoposti ad opportuni calcoli che vedremo in un prossimo articolo di esempio di fabbricazione di uno specchio 200F6, forniscono le quantità di aberrazione e le posizioni in cui correggerle per ottenere un ottica perfetta.
(Col termine aberrazione si intende in pratica l’errore che deve essere corretto, ma che ora si trova presente sulla nostra curva in esame, rispetto alla curva di una parabola teorica presa come riferimento costruttivo).
Si procederà quindi a realizzare una maschera di Couder (vedi articolo specifico in questo blog) in cartone, con un certo numero di finestre coincidenti con le corone circolari da misurare. Tale maschera verrà anteposta allo specchio posto su un supporto con la superficie riflettente in verticale.
Si installa poi il tester di Foucault (del tipo di quello mostrato nell’articolo dal titolo “setup del test di Foucault “), che deve essere perfettamente allineato sull’asse ottico dello specchio, ad una distanza il più possibile vicina alla lunghezza del raggio di curvatura che ci si aspetta abbia lo specchio.
In seguito si eseguirà la ricerca del centro di curvatura di ogni zona, a partire da quella centrale, annotando il relativo tiraggio. E via via cercando la tinta piatta (alias il centro di curvatura) dentro ogni coppia di finestre che individuano una corona circolare dello specchio, annotandone il tiraggio relativo rispetto alla zona precedente.
ATTENZIONE perché la zona centrale è un punto molto delicato ed importante del lavoro: Essa è il luogo di partenza cui si riferiranno tutte le seguenti misure relative da zona a zona, ed è quindi la più importante perché sbagliando quella ci porteremo dietro l’errore su tutte le altre zone.
Tutto ciò, e quanto segue, la rende la zona in cui è più difficile trovare con certezza la reale tinta piatta.
La difficoltà nasce dal fatto che la zona centrale è la più ampia ma è pure la meno deformata, e quindi comporta che occorra spostare longitudinalmente sull’asse ottico il carrello del tester di una maggiore quantità rispetto a tutte le altre zone che saranno esaminate, ma il grave è che in tale grande spostamento pare sempre che l’ombra visibile cambi di poco o nulla (e ciò è dovuto alla poca deformazione della zona), rendendo quasi impossibile avere la certezza della reale “tinta piatta” raggiunta.
Ogni operatore che incappa in quell’incertezza si crea delle sue regole personali per trovare l’esatto centro di curvatura della zona centrale. La mia regola è la seguente:
– Spostare il carrello del tester in una zona francamente intrafocale e introdurre la lama (operando con la sua vite di regolazione) in modo tale che essa raggiunga esattamente il centro dello specchio, e annotare il tiraggio di quel punto di partenza.
– Lasciare la lama in quella posizione e indietreggiare col carrello finchè non si renda visibile l’ombra della lama speculare rispetto al punto di partenza.
Praticamente durante lo spostamento del carrello si renderà visibile la progressione dell’ombra verso sinistra fino allo scurimento totale; il quale perdurerà per alcuni mm del continuo indietreggiamento, ed in seguito l’ombra comincerà a schiarire la parte destra dello specchio fino a mostrare la posizione dello specchio speculare rispetto alla partenza. Posizione in cui ci si deve arrestare.
Annotare il tiraggio di quel punto di arrivo.
Per differenza delle due letture dei valori di tiraggio, si trova la distanza percorsa col carrello del tester. Dividerla quindi per due per trovare la mezzeria e spostare il carrello in quella posizione mediana.
Se tutto è andato liscio (e se il tester era perfettamente in asse coll’asse ottico dello specchio), quella è la posizione che più facilmente rappresenta il vero centro di curvatura della zona centrale.
La serie di misurazioni parte quindi da quella zona al centro dello specchio e, procedento a valutare ogni coppia di finestre della maschera di Couder, arriva alla zona periferica. Dopodiché si esegue una nuova serie di misure scendendo dalla zona periferica al centro.
Si avranno quindi a disposizione due valori di tiraggio per ogni zona misurata, e di tali valori sarà calcolata la media, il cui valore verrà utilizzato nei calcoli di valutazione della qualità della parabola.
A questo punto occorre considerare che il test di Foucault, come tutti gli altri tests ottici eseguibili a livello amatoriale (quindi senza hardware sofisticato e/o complicato) risente di possibili errori SOGGETTIVI di gravità inversamente proporzionali alla esperienza dell’esecutore.
L’unica sicura riduzione di quel tipo di errore viene quindi dall’utilizzo di valori MEDIATI su un certo numero di misure. Più sono le misure, e più il loro valore medio è rappresentativo del vero valore reale.
Detto questo, E’ BUONA COSA CONSIGLIABILE SPECIE AI NEOFITI che vengano eseguite più nuove sessioni di misurazioni in “andata e ritorno”, al fine di avere a disposizione almeno quattro valori (due in “salita” e due in “discesa”), sui quali calcolare una media che correggerà già di molto quell’eventuale errore soggettivo.
(Ognuno in “cuor suo” conosce la sua bravura, e si comporta responsabilmente di conseguenza).
LA SENSIBILITA’ DEL TEST DI FOUCAULT
è elevatissima, poiché un semplice tester costruito in modo artigianale con pochi pezzi di legno, è storicamente ritenuto in grado di amplificare un difetto ottico di un fattore seicentomila. Pertanto nelle misurazioni delle parabole si possono eseguire sul vetro correzioni manuali tali da portare il valore dell’errore cosiddetto “picco/valle”, a molto meno del “minimo sindacale” di qualità “entry level” , costituito dal valore di 68.75 nanometri (cioè milionesimi di millimetro) che è un ottavo della lunghezza d’onda della luce verde a cui l’occhio umano è più sensibile, al di sopra del quale errore un difetto dell’ottica si mostrerebbe visibile.
Ricordando che un errore sul vetro pari a Lambda/8 affligge doppiamente l’onda riflessa, una prima volta in incidenza, ed una seconda in emersione, generando sull’onda riflessa un errore complessivo di (1/8+1/8)=1/4 Lambda, che si esprime notoriamente come Lambda/4, e che si ritiene il livello di ingresso di una buona qualità considerabile limitata dalla sola diffrazione.
PROSSIMAMENTE seguirà un altro articolo contenente un esempio completo di lavorazione di uno specchio 200F6 con la sequenza completa delle dieci sessioni dei test di Foucault e relative correzioni che si sono rese necessarie per portarlo dal valore di qualità iniziale di lambda/1.3 al valore di qualità finale di lambda/10.4 . Ad un valore cioè molto migliore del valore di lambda/4 che rappresenta il già citato “minimo sindacale”di qualità appena passabile per un ottica riflettente.