Che cos’è il test ottico “della Caustica”.

E’ un test nato nel 1939 e serve a misurare con estrema precisione (impossibile al test di Foucault) i raggi di curvatura delle zone di uno specchio parabolico, o di figura ancora più deformata da quella parabolica, avente un rapporto focale molto corto (cioè decisamente inferiore ad F5) e un diametro oltre i 300 o 400mm, per guidare l’ottico alla sua perfetta correzione in fase di costruzione.

E’ un metodo più “spartano”, antico, meno impegnativo e meno costoso in termini di hardware del fotografico test di Hartmann degli anni 1960, ed è quindi più accessibile all’uso amatoriale.

Anche il test di Roddier (descritto in altro articolo del presente blog), è soggetto alle stesse complicazioni hardware dell’Hartmann, ma ha lo svantaggio capitale di essere utile solo a fornire la precisa valutazione qualitativa di una ottica già terminata. E pertanto non è utilizzabile allo scopo di guidare alla massima correzione necessaria nella fabbricazione di un nuovo specchio.

La trattazione del test della Caustica è destinata per sua natura ad una ristrettissima cerchia di molto specifici amatori. Non per nulla essa è apparsa (dal 1935 ad oggi) a livello mondiale in pochissimi documenti, due dei quali sono i seguenti:

1. Il testo tratto dal libro “Amateur Telescope Making”, volume 1 (la mia è la seconda edizione del 1998), con un articolo, ovviamente in lingua inglese, scritto da Irvin Schroader dell’ Applied physics laboratory della Johns Hopkins University (Baltimora – Maryland – USA);
2. ed in un apposito capitolo contenuto nell’ottimo libro in lingua francese dal titolo “Realisez votre telescope”, di Jean Marc Lecleire (la cui mia edizione è del 1997-1998).

Ambedue queste fonti sono redatte nelle lingue dei Paesi d’origine, dove l’autocostruzione ottica amatoriale era (a fine secolo scorso, nel tempo dei miei studi da amatoriale “grattavetro”… Ma forse lo è ancora oggi), certamente più diffusa che in Italia, dove di conseguenza un testo guida italiano sul test della Caustica risulta tuttora, a distanza di 17 anni, irreperibile (anche per l’indole tutta italiana “di massima entropia”, ovvero di scegliere il “più naturale e meno faticoso soprassedere”, optando piuttosto per l’acquisto del “più costoso” perchè fatto da altri, che viene erroneamente percepito come migliore).

Perciò, da curioso e “addetto ai lavori”, in conseguenza di un mio primo timido e non approfondito approccio pratico (ecludente gli “aiuti” di dubbia qualità provenienti dai Forum, ed a favore della classica, sana ed autorevole lettura di libri) ricordo di aver tradotto in italiano un riassunto dei concetti tecnici che lo definiscono, come mia guida operativa iniziale immediatamente accessibile.

Naturalmente a mio uso, e di quei pochissimi auto-costruttori che come me non disdegnano il coinvolgimento attivo , e che forse potranno trarne qualche vantaggio.

L’apparecchio tester per condurre il test della caustica è una variante più complessa del tester di Foucault, necessitando rispetto a questo, di una precisa e micrometrica misurabilità ANCHE sull’asse ortogonale (asse Y diametrale dello specchio), oltre alla precisa misurabilità longitudinale lungo l’asse ottico (X) dello specchio.

In pratica, mentre nel test di foucault l’operatore stabilisce che il raggio di curvatura di una certa zona dello specchio è raggiunto quando egli vede comparire contemporaneamente in coppie di finestre diametrali della maschera di Couder, quella che valuta come “tinta piatta” , Nel test della caustica, per il motivo che vedremo, egli dovrà più impegnativamente calcolare dapprima le precise coordinate X di ogni singola finestra delle due che rappresentano ciascuna zona dello specchio in esame, ed andarne poi a misurare le coordinate Y.

La caratteristica diciamo..”REGINA” è però che il test della caustica NON E’ SOGGETTIVO quanto intrinsecamente  lo è il test di Foucault, per il fatto che l’operatore NON deve come nel Foucault giudicare a occhio l’eguaglianza delle ombre di due finestre diametrali; MA deve bensì individuare l’immagine della caustica della fenditura in una sola finestra alla volta, di ciascuna zona.

L’immagine utile della caustica di tale fenditura si presenta in modo incontrovertibile come una NETTA linea chiara su sfondo lattiginoso.

Potrei dire che non si tratta infatti della reale immagine della fenditura, ma del complesso di assenza di linee di diffrazione che la caratterizzano in quel solo punto focale, ove viene mostrata netta e pulita come una linea verticale luminosa, come quella rappresentata in figura.

Immagine ben distinguibile da quella non più netta ma sfocata, che la fenditura mostrerebbe di sé quando fosse intercettata col tester in una posizione ancora intrafocale.

O per converso quando essa fosse intercettata in una posizione già extrafocale, presentandosi via via bordata di frange di interferenza, fino a sdoppiarsi.

Il test della caustica è nato da uno studio del 1939 che i due astronomi e fisici argentini Richard Platzeck e Enrique Gaviola, pubblicarono sul Journal of the optical society of America.

Questo test ebbe come autorevole “battesimo” la prestigiosa costruzione iniziata nel 1936 dell’avveniristico telescopio Hale installato all’osservatorio del Monte Palomar (San Diego California) gestito dal “CalTech”.

Quel telescopio è un Cassegrain con diametro 5,08 metri e rapporto focale F3,38, entrato in servizio nel 1948 e rimasto il più grande telescopio del mondo fino al 1976.

Lo specchio del peso di circa 14 tonnellate venne ottenuto fondendo il nuovissimo vetro Pirex a bassa dilatazione termica, brevettato nel 1919 dalla Corning Glass statunitense. Mai in precedenza fuso in monoblocchi di tale mole che presentano i rischi di frattura fragile da raffreddamento non omogeneo della grande massa vetrosa.

Il lavoro di smerigliatura per lo scavo della curva durò 13 anni con l’asporto per abrasione, delle ben 5 tonnellate di vetro, necessarie per raggiungere la desiderata profondità di freccia di poco meno di 100mm.

MOTIVI PER CUI IL TEST DI FOUCAULT E’ IMPRECISO PER LE CORTE FOCALI

Ricordando per i neofiti che la costruzione di uno specchio parabolico inizia sempre con la più facile realizzazione di una superficie sferica, la cui luce riflessa però non porta a convergere in un solo punto focale tutti i raggi provenienti da un oggetto posto all’infinito, come è necessario per compiere La funzione telescopica. Pertanto la immagine al fuoco è inutilizzabile perché si presenta come una macchia formata dalla sovrapposizione di infinite immagini non coincidenti.

Per costruire un obiettivo riflettore da telescopio occorre che la superficie sferica dello specchio sia poi lavorata e deformata “svasandola” nella forma di parabola, che si differenzia dalla forma sferica per non possedere un unico raggio di curvatura della superficie, ma di possederne uno che aumenta in modo progressivo e continuo, secondo la formula matematica che definisce una teorica e perfetta parabola di riferimento, con un raggio che è minimo al centro dello specchio, e massimo al bordo.

Tale raggio continuamente crescente permette di mettere a fuoco e formare in un solo punto focale l’immagine dell’oggetto all’infinito. Immagine molto piccola che verrà osservata con oculari che permettono di ingrandirla di un numero di volte pari al rapporto fra la lunghezza focale dello specchio e quella dell’oculare.

Nella pratica della realizzazione di uno specchio parabolico, la misurazione precisa dell’aumento progressivo e continuo dei raggi di curvatura di una parabola, era ed è, cosa impossibile se non si ricorre all’espediente di compromesso semplificativo di suddividere lo specchio in corone circolari tanto più ristrette quanto più si procede verso il suo bordo dove la variazione del raggio è più repentina.

Nel test di Foucault per valutare quale sia la misura di quel loro raggio di curvatura si assume quindi che ciascuna di quelle fittizie corone circolari abbia un “raggio comune”, ovvero le si tratta come se quell’anello di vetro di limitata larghezza avesse superficie sferica.

In quel test quindi, l’individuazione della lunghezza del raggio avviene quando ad un certo punto del movimento longitudinale (tiraggio) del carrello del tester, alla introduzione della lama nel cono di luce riflessa, appare all’occhio dell’operatore (contemporaneamente in ambedue le finestre della maschera di Couder aperte sul diametro che individua quella corona) la “tinta piatta” dell’ombra.

La tinta piatta si ha solo quando l’ombra è percepita non proveniente né da destra né da sinistra, ma come dalla chiusura di un diaframma di 360 gradi. Questo fenomeno avviene solo quando ci si trova “più o meno” nel centro di curvatura di quella zona fittizia, ovvero quando ci si trova con la lama del tester ad una distanza dallo specchio pari al raggio di curvatura che “assumiamo comune” per quella superficie in esame.

Nel considerare quelle corone circolari aventi raggio comune, si compie però un errore soggettivo tanto più trascurabile e meno dannoso quanto più lo specchio possiede una parabola poco deformata, cioè poco differente dalla sfera, ovvero con rapporto focale elevato (da F5 – F6 a salire).

Ma nell’esame delle focali più corte di F5 quell’errore soggettivo diventa via via troppo grande, cominciando ad essere misurabile da diametri di specchio superiori a 300mm, e diventando via via più importante e dannoso, perchè il centro di curvatura dei raggi delle parabole di corta focale cadono sull’asse ottico solo per la zona centrale, mentre (come vedremo nel capitolo seguente) per le altre zone essi cadono su una curva caustica che si allontana sempre più dall’asse ottico, man mano che si raggiunge il bordo dello specchio, ovviamente danneggiando maggiormente la qualità dello specchio in funzione del crescere del suo diametro.

Per quelle corte focali invece il metodo della caustica è risolutivo, in quanto come già accennato non si valuta più ad occhio e soggettivamente la qualità di un’ombra che compare contemporaneamente sulle due finestre diametrali, ma di ogni corona circolare si prende in considerazione la immagine della caustica prodotta da una sola finestra alla volta, pre calcolandone le coordinate  X, e posizionadoci su di esse per misurare le coordinate Y di distanza reciproca delle due finestre.

Con la rilevazione delle coordinate X e Y di ogni zona, il metodo di misurazione “della caustica” risulta tanto più preciso quanto è maggiore l’aberrazione longitudinale al centro di curvatura (col termine aberrazione si intende la deformazione rispetto alla sfera). Caratteristica propria delle corte focali cioè delle parabole profonde o di iperboli.

Per questo motivo il test della caustica è un test non applicabile agli specchi sferici o parabolici di lunga o media focale, cioè aventi minima aberrazione rispetto alla sfera, perché le coordinate X e Y sarebbero talmente piccole da non essere misurabili, confondendosi con la sfera stessa. Pertanto risulta ugualmente di applicazione assai difficile o impossibile a fine lucidatura quando si comincia la parabolizzazione e la superficie non è ancora parabolica ma solo sferoide.

Normalmente viene consigliato di iniziare e mantenere le misurazioni col test di Foucault, fino a che lo specchio non arrivi a possedere una figura parabolica con precisione molto vicina a lambda/4 (errore massimo picco/valle sul vetro pari a 68,75 milionesimi di millimetro).

Ma a quel punto della lavorazione (che normalmente contraddistingue il raggiungimento della qualità minima “entry level” lambda/4 per uno specchio di focale uguale o maggiore di F5), lo specchio di corta focale  a lambda/4  risultanti col Foucault NON è ancora terminato.

Si inizia quindi solo da quel risultato in poi, ad applicare proficuamente il test della caustica, che guiderà alle successive precise correzioni fino al termine della lavorazione impeccabile dello specchio. 

Accontentarsi o continuare oltre con l’inadeguatezza del test di Foucault sulle corte focali, vorrebbe dire stimare milionesimi di millimetro tirando a indovinare, invece di misurare ed essere guidati a realizzare la reale curvatura dello specchio, ed è una scorciatoia o un malcostume assai poco professionale, che può magari soddisfare il proprio “Fai Da Te” per un uso visuale del telescopio, ma la cui scarsa qualità ottica si può scoprire sottoponendo lo specchio ad un un test qualitativo profondo, come si ottiene ad esempio con il test di Roddier descritto in un  apposito articolo, anche quì in Grattavetro.

E’ noto che i telescopi Newton di grande diametro e corta focale sono nati per avere comodità di accesso all’oculare senza dover utilizzare una scaletta, e siccome i grandi diametri di specchio favoriscono la visione ad altissimo ingrandimento di piccoli particolari sulla superficie dei pianeti, o la separazione di stelle doppie assai vicine, la eventuale scarsa qualità dello specchio primario realizzato col solo test di Foucault viene anche percepita dapprima con sospetto, e in seguito con certezza dall’occhio dell’astrofilo smaliziato, ed in seguito di solito confermata dai test qualitativi più profondi.

E visto che la tendenza dei desideri degli astrofili e della tecnologia vanno nel senso dei grandi diametri di specchio primario, e quindi delle comode corte focali,  è bene che chi desidera ordinare uno specchio si sinceri che lo specchio non sia realizzato col solo test di Foucault, per evitare di incorrere prima o poi in quel sospetto iniziale che nasce con l’uso del telescopio, e che viene spesso confermato dai test approfonditi. E vista la evidente diffusione di specchi di corta focale e scarsa qualità, questa è la ragione per la quale molti astrofili smaliziati che non li amano, preferendo utilizzare la solita vecchia scaletta.  

IL FUNZIONAMENTO DEL TEST DELLA CAUSTICA, e il perchè esso è migliore del test di Foucault.

Ci aiuteremo osservando alcune figure:

Guardando questa immagine che si riferisce al riflesso prodotto da un’arbitraria corona circolare comprendente le finestre a e b della superficie di uno specchio parabolico, troviamo raffigurati i due assunti teorici che stanno alla base del test di Foucault; e cioè che:

1. Per le citate ragioni pratiche di misurazione, si considera sferica (cioè mono raggio) ogni piccola zona di superficie (comprese quindi le nostre superfici arbitrarie “a” e “b”, indipendentemente dal fatto che in realtà la superficie dello specchio sia parabolica o addirittura di maggiore deformazione).
2. Si ritiene che le riflessioni di ogni corona circolare cadano “sempre” sull’asse ottico dello specchio; Quindi il riflesso prodotto dalla zona centrale dello specchio cade nel punto indicato in figura come “centro di curvatura della zona centrale”, che rappresenta il vero, Ma anche il riflesso prodotto dalla zona che contiene le finestre “a” e “b” è considerato cadere sul medesimo asse, e ciò invece non è vero.

O meglio, è stato dimostrato che ciò è trascurabilmente molto vicino al vero solo per le lunghe focali, ma non lo è per le focali corte proprie degli specchi molto deformati, poiché portando in “tinta piatta” col test di Foucault due finestre abbastanza periferiche “a” e “b”, e togliendo poi la maschera di Couder, si noterà in realtà che l’ombra “piatta” della lama, dapprima mostrata attraverso le finestre, si muove invece concordemente col movimento della lama stessa, dimostrando che non ci si trova ancora nel perfetto centro di curvatura, ma ci si trova ancora in posizione intrafocale.

Ci aiuterà anche qui la prossima immagine:

Lo studio dei Platzeck e Gaviola fu teso quindi a realizzare un metodo per poter misurare la posizione esatta dell’effettivo fuoco riflesso da ogni zona (comprese le nostre ipotetiche zone “a” e “b”). Trovando che per esse il centro di curvatura non cade sull’asse ottico dove i due riflessi lo incrociano, ma cade nei punti A e B che si trovano a una precisa e pre-calcolata distanza X dal punto C, dove cade unicamente il riflesso della zona centrale dello specchio e ha sede la cosiddetta punta della caustica, ovvero inizia la curva caustica tratteggiata, e quei due riflessi sono separati radialmente da una distanza Y.

Le distanze di X e di Y dall’asse ottico, come si vede dalla curva punteggiata, sono tanto maggiori procedendo verso il bordo specchio, quanto più esso ha corta focale.

E questi punti, per le varie zone, giacciono tutti progressivamente lungo quellaa curva punteggiata a forma di padiglione di tromba indicata della immagine qui sopra, che ha inizio sull’asse ottico solo per il punto C, dove cade solamente il riflesso della zona centrale dello specchio.

PREPARAZIONE TEORICA AL TEST

Si tratta di prendere atto che occorre misurare in modo molto preciso (almeno al centesimo di millimetro), le coordinate X e Y del centro di curvatura di ogni zona.

Facendo riferimento alla figura seguente (ovviamente in scala esagerata per ragioni di comprensibilità del fenomeno) ci addentriamo nel principio del test, e vediamo che una sorgente luminosa formata da una fenditura, è installata al centro di curvatura della zona centrale C di uno specchio parabolico, ed illumina le due piccole regioni a e b, poste ad “altezza” h dall’asse centrale della superficie dello specchio.

(In ottica si usano fenditure perché molto più facili da realizzare. Si parla ad esempio di larghezza 20 o 30 micron, ove la realizzazione di un foro stenopeico di quei diametri è molto più difficile, pur presentando sia il foro che la fenditura le medesime proprietà fisiche, col notevole e comodo vantaggio di una maggiore visibilità di quest’ultima)

Sperimentalmente Platzeck e Gaviola riscontrarono che l’immagine della fenditura a fuoco non era riscontrabile in P, come assunto dal test di Foucault, ma occorreva spostarsi ulteriormente in posizione via via fuori asse, e giacente su punti che costruiscono le due linee punteggiate descriventi la curva a campana. Nel nostro caso il preciso punto di fuoco delle finestre periferiche a e b si trova nei punti A e B simmetrici all’asse ottico, ma non giacenti su di esso.

Tutti i punti della superficie dello specchio parabolico obbediscono a questa regola, ad eccezione del primo punto relativo alla zona centrale dello specchio, che è l’unico a cadere in C sull’asse ottico.

Venne quindi stabilito che ai fini della misurazione precisa dei tiraggi e delle focali derivanti, che interessano il “mirror maker ” alias “grattavetro”, si chiama X la distanza sull’asse ottico (in figura è orizzontale) fra l’estremità C, (ove si trova la “PUNTA” inizio della curva caustica), e la proiezione sull’asse ottico dei punti A e B di ogni zona da misurare.

Altrettanto si chiama Y la distanza (che nel disegno è verticale) che separa i punti A e B.

Con le seguenti due formule si calcolano quindi preventivamente i valori teorici delle coordinate X e Y posseduti da una perfetta parabola di riferimento, che si usa come confronto e guida alla realizzazione del nostro specchio:

Dove R è il  raggio di curvatura della zona centrale dello specchio, e H è l’altezza sull’asse verticale della zona misurata.

Qualora il tester fosse costruttivamente del tipo con la sorgente fissa, cioè indipendente dal movimento del carrello longitudinale (sul quale quindi la sorgente NON si sposta lungo l’asse longitudinale durante le misurazioni), occorrerebbe moltiplicare per 2 i valori X e Y ottenuti.

CARATTERISTICHE DEL TESTER

Il tester conserva il carrello longitudinale del tester di Foucault, ma presenta una nuova slitta ortogonale, in sostituzione di quella basculante che per il Foucault portava la lama.La nuova slitta sosterrà un oculare, ad esempio da 9mm di focale, avente reticolo verticale o a croce, l’orientamento del quale deve essere allineato alla fenditura

L’oculare serve per ingrandire la immagine caustica della fenditura formata nel fuoco di ciascuna zona dallo specchio, per poterne meglio apprezzare l’esatta nitidezza e posizione.L’ingrandimento è dato dalla formula:

Ingrandimento =1000/(4f) = 1000/(4×9)= 1000/36=28 volte

Nel nostro esempio l’oculare (di cui f rappresenta la focale) ingrandisce 28 volte.

Il carrello di spostamento laterale deve essere dotato di una vite micrometrica o di un comparatore con precisione del micron, o in difetto, almeno i dieci micron del centesimo di millimetro.

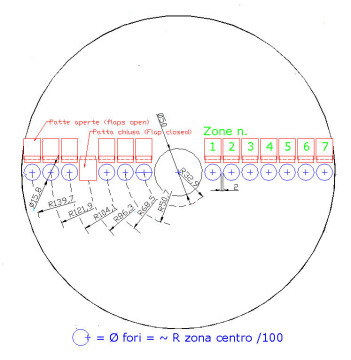
Si realizza quindi uno schermo (una maschera) circolare rigido in cartoncino bristol o in legno compensato, provvisto di tante coppie di fori tondi, praticate sul diametro,quante sono le zone da misurare, lasciando uno spazio di separazione di 2 mm fra i fori contigui. Schermo che sarà posto in verticale davanti allo specchio,

Il diametro dei fori è previsto in circa un centesimo del raggio R di curvatura della zona centrale dello specchio: Per uno specchio con R=1800mm il diametro è quindi circa 18 mm, ma il suo valore reale non è critico,e sarà determinato in modo più preciso dalla suddivisione ottimale delle zone in cui sarà possibile suddividere equamente il diametro dello specchio.

Il numero dei fori deve ovviamente essere intero, pari, e ripartito equamente sulle due metà del diametro specchio, con la zona più esterna tangente il bordo esterno.

Nel caso di uno specchio col centro forato, le due finestre più interne è consigliato che siano distanziate dal foro di qualche mm, per non avere una misurabilità disturbata da una spuria e luminosa riflessione estranea proveniente dal bordo del foro.

Dopo aver realizzato la maschera occorre realizzare degli sportellini numerati destinati a chiudere le finestre che al momento non servono, e fissati al di sopra dei fori con nastro adesivo, e chiusi o aperti alla minima pressione di un etichetta “post-it”, in modo da poter essere agevolmente e delicatissimamente chiusi o aperti SENZA MUOVERE MINIMAMENTE maschera e specchio sul suo supporto.

Il seguente è il solo esempio pratico rintracciabile in letteratura, di conduzione del test, e si trova nel volume di Lecleire citato più sopra.

Esso riguarda uno specchio diametro 300 mm con 7 coppie di finestre diametro 15.8 mm. (rapporto di ampiezza = 1/114 R) con spaziatura interforo di 2 mm

I raggi “hm” delle varie zone sono indicati in figura 4

LA PRATICA DEL TEST DELLA CAUSTICA, LE REGOLAZIONI:

Dopo aver installato lo specchio sul suo supporto senza schermo, occorre piazzare il tester al centro di curvatura e accendere la sorgente luminosa. L’immagine di ritorno della caustica prodotta dalla fenditura riflessa dallo specchio deve proiettarsi all’interno dell’oculare.

Si agisce quindi sulle viti di regolazione del supporto dello specchio per centrare in altezza l’immagine della fenditura all’interno dell’oculare.

La larghezza di una fenditura utile è indicata in circa 20 o 30 micron. Il reticolo dell’oculare deve essere parallelo ad essa.

Procedere poi all’allineamento dell’asse longitudinale del tester con l’asse ottico dello specchio, realizzando e anteponendo a questo un nuovo schermo circolare di pari diametro e provvisto di tre fori diametrali allineati: Uno al centro e gli altri ai bordi opposti.

Sistemato lo schermo davanti allo specchio si osserveranno all’oculare tre diverse immagini della fenditura, ciascuna proveniente da un foro della maschera. Spostando il carrello del tester lungo l’asse ottico, si constata che le immagini laterali si avvicinano o allontanano a quella centrale, a seconda del senso dello spostamento.

Al punto di intersezione dei due fasci luminosi riflessi dalle zone periferiche con l’asse ottico, le immagini laterale si sovrapporranno confondendosi con la immagine centrale. Poi si sdoppieranno nuovamente se si continuerà con lo spostamento longitudinale del carrello del tester.

Se si constata che l’immagine centrale si sposta lateralmente, occorre correggere l’orientamento dell’intero tester, sia in senso longitudinale che centrando meglio il carrello ortogonale.

Quando l’oculare è allineato con l’asse ottico dello specchio, in qualsiasi posizione venga spostato il carrello longitudinale le due immagini si muovono simmetriche ed opposte (a sinistra e a destra del reticolo dell’oculare) sull’asse ottico materializzato dalla immagine centrale che rimane perfettamente ferma.

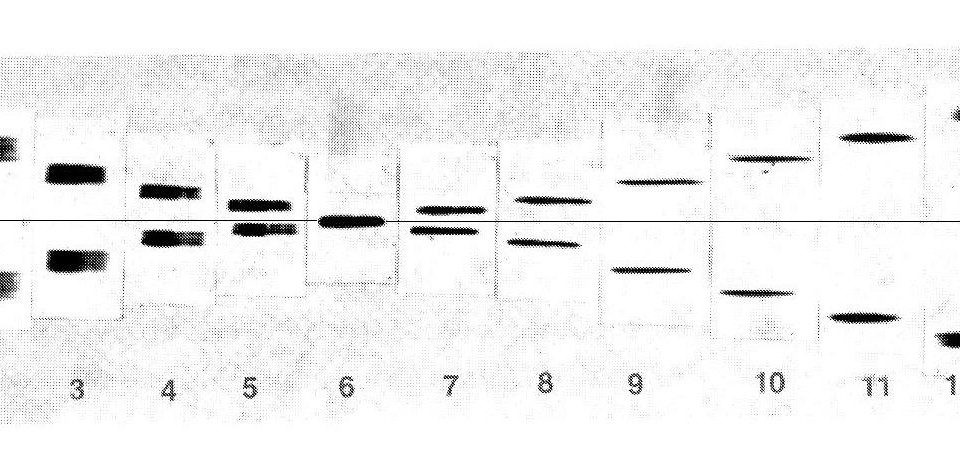
Per una maggiore comprensione dell’andamento del test, tolta la maschera di allineamento, e sostituita con la maschera di misura dotata dei fori delle zone, in ambedue i testi riferiti più sopra si fa ricorso alla seguente immagine.

La figura mostra da destra a sinistra n.13 fotografie della fenditura riflesse dalla medesima coppia di finestre a e b praticate su una zona perfierica come indicato in figura 3, scattate spostando il tester lungo l’asse ottico dello specchio.

La foto 1 è eseguita nel punto C, al centro di curvatura della zona centrale: L’immagine della fenditura è doppia e sfocata perché siamo in posizione francamente intrafocale rispetto alle finestre a e b che invece sono aperte su una zona periferica.

La foto 6 è eseguita nel punto P sull’asse ottico: Le due fenditure sono quasi sovrapposte ma ancora fuori fuoco. Questo sarebbe il punto dove il test di Foucault ci fornirebbe la tinta piatta individuante il fuoco.

Ma il vero fuoco e la nettezza della figura della caustica della fenditura, la troviamo solo nella foto fatta in posizione n. 9, col seguente aspetto visto all’oculare:

L’immagine è trovata alla distanza di quella posizione, muovendo il carrello laterale del tester. Procedendo oltre quel punto le immagini torneranno ad allontanarsi e ad andare in extrafocale.

LA PIU’ IMPORTANTE REGOLAZIONE

Consiste nell’identificare l’esatto punto di inizio della Caustica da cui iniziare le misurazioni, rintracciando l’immagine della fenditura netta come vista qui sopra, nella posizione del punto C di figura 3 corrispondente al riflesso della prima zona.

Siccome tutte le misure successive dipenderanno da quel valore, occorre che esso sia identificato con la massima precisione (almeno 2 o 3 centesimi di mm).

LE MISURE

•  Si è già anticipato che occorre preventivamente calcolare i valori teorici di X e di Y Con le formule X=3H^2/2R e Y= 2H^3/R2, .
•  A ciascun valore calcolato di X si aggiunge il valore iniziale letto sulla vite micrometrica al punto C di inizio caustica ottenendo il valore X corretto. (E’ il valore di riferimento di tutte le misure, ed è per questo importante la sua massima precisione).
• Aprire quindi solo la finestra di sinistra della zona 1.
• Portare l’apparecchio sul valore teorico X corretto della zona corrispondente.
• Centrare con cura il reticolo dell’oculare sulla immagine della fenditura a annotare il valore Y sinistro (Ysx) letto sul nonio della vite di spostamento laterale-
• Senza muovere né apparecchio e né specchio, chiudere la finestra di sinistra e aprire quella di destra.
• Centrare nuovamente la immagine della fenditura sul reticolo agendo solo sullo spostamento laterale, annotare il valore Ydx letto sulla vite micrometrica.

Ripetere queste operazioni per tutte le zone, sapendo che a partire dalle zone di altezza circa 0.4 volte il diametro in genere si possono aprire contemporaneamente ambedue le finestre perché le due immagini da quella posizione in poi seguendo la curvatura a tromba saranno più distanziate e non più interferenti per sovrapposizione.

INTERPRETAZIONE DELLE MISURE

Lo scopo delle misure è quello di verificare se, e dove è necessario intervenire con correzioni che asportino l’eventuale vetro in eccesso, per far si che lo specchio rispetti i seguenti criteri che sono interdipendenti ed indispensabili:

1) Lord Raileigh (per estensione del suo concetto fisico espresso sull’onda) stabilì che la massima grandezza di un difetto su una superficie ottica, in grado di cominciare a portare danni alla immagine di diffrazione o raggio di Airy, ha la misura di un ottavo della lunghezza d’onda (Lambda) della luce giallo-verde a cui l’occhio umano è più sensibile, poiché durante la riflessione l’onda verrebbe danneggiata due volte, una in incidenza ed una in riflessione, portando il danno complessivo al valore di (1/8 +1/8 = ¼) = Lambda/4.

Un tale difetto causa la perdita di luminosità al centro della immagine di diffrazione, per disperderla negli anelli adiacenti, “allargando” il punto luminoso in una “macchia”, con deterioramento di contrasto generale.

Nel nostro caso si verifica visualmente su un apposito grafico, quali siano i punti in cui intervenire con correzioni, affinché la linea spezzata che rappresenta l’andamento della riflessione delle zone del nostro specchio, si avvicini il più possibile ai valori della parabola di riferimento, con uno scarto massimo ammissibile che non deve essere superiore appunto a Lambda/4

2) Couder richiede che i raggi luminosi riflessi da tutte le zone della nostra parabola convergano all’interno del detto raggio di Airy, cioè il disco di formazione della immagine. In altre parole, occorre che tutte le zone della nostra parabola partecipino alla formazione della immagine di diffrazione poichè se una o più zone riflettessero la loro parte di luce al di fuori di quel raggio geometrico, la immagine fornita dal telescopio non presenterebbe la forma canonica presa in esame da Lord Raileigh, col deterioramento di contrasto generale indicato nel precedente punto.

Nel nostro caso si verifica visualmente su altro apposito grafico, quali zone eventualmente riflettano fuori del raggio di Airy, per poterle correggere facendole rientrare all’interno del medesimo.

Detto ciò, ci si attrezza per le misurazioni preparando un foglio con colonne destinate ad accogliere i valori di X e di Y teorici, oltre che i valori di Ydx e Ysx misurati.

Annotare come Ym la differenza fra Ydx e Ysx per ciascuna zona dello schermo;

calcolare infine le misure “Ridotte” corrispondenti a quelle misure grezze, utilizzando la seguente formula:

Misure Ridotte = (Y-Ym) R/2hm

Dove R = Raggio di curvatura al centro dello specchio, e con hm = altezza media di ogni zona.

A partire da queste misure Ridotte si calcolano le aberrazioni:

Aberrazione Longitudinale al Centro di curvatura Alc; e

Aberrazione Trasversale al Fuoco Atf

utilizzando le stesse formule usate per il test di Foucault, che sono le seguenti:

Alc= Misure Ridotte – K

Atf= Alc • hm/2R

Dove K è una costante positiva o negativa ottenibile per prove successive, che va scelta in modo tale che il valore Atf di ogni zona, diviso per il raggio della tacca di diffrazione dello specchio, dia un valore inferiore alla unità (il che in pratica significa che se ciò avviene, il raggio di luce incidente viene riflesso a distanza focale all’interno del piccolissimo raggio di Airy).

Nota chiarente il ruolo della costante K, e il risultato del suo uso, ottenuto con un solo colpo d’occhio su un grafico

Allo stesso modo con cui si opera eseguendo un test di Foucault, Anche col test Caustica, per verificare lo scostamento della curva parabolica grezza che stiamo costruendo rispetto a quella teorica presa come riferimento costruttivo, dobbiamo immaginare di “sovrapporre” le due curve.

La sovrapposizione serve per riuscire a vedere dove sono, e quanto sono ampie, le sporgenze di errore che differenziano la nostra curva da quella di riferimento, in modo da poter correggere la nostra con opportuni ritocchi.

Ma una sovrapposizione materiale non è possibile con i nostri due oggetti che sono solo numerici, ma è quindi possibile sovrapporli con una simulazione matematica.

Il foglio di calcolo calcolerà quindi per ogni zona una sua costante K. e avremo quindi a disposizione tante costanti K quante sono le zone di test in cui è divisa la curva, e potremo quindi matematicamente sovrapporre, le due curve, zona per zona, una alla volta, prendendo come punto di contatto di volta in volta una diversa zona. Contatto che nel foglio di calcolo è simulato sottraendo a tutte le altre zone il valore della costante K della zona al momento presa in esame.

Tutta l’operazione non ecessita che di scegliete nel foglio di calcolo i valori di una costante k alla volta e guardare a colpo d’occhio il grafico risultante dal nuovo andamento della curva. E quindi scegliere quale zona prendere come punto di contatto conveniente , in base alla nostra esperienza, al tempo di lavoro, alla nostra abilità ed alla minima quantità di vetro da asportare,  per realizzare una parabola perfetta, identica a quella di riferimento.

A chi fosse interessato vedere una tale simulazione di esempio con i grafici commentati ad illustrare pro e contro, suggerisco di leggere questo breve articolo:

https://www.grattavetro.it/200f6-studio-sul-1-test-di-foucault/

Fine della nota sulla costante K

UNA CONSIDERAZIONE SUL RAGGIO DELLA TACCA DI DIFFRAZIONE,

Che, detta anche Centrica, oppure Raggio di Airy, si calcola con la nota formula:

Raggio di Airy = 1.22 * lambda [in micron] * (f/ D)

Dove lambda è la solita lunghezza d’onda della luce giallo-verde cui l’occhio è più sensibile (550 nanometri, ovvero 0.56 micron); ed f è la lunghezza focale dello specchio e D il suo diametro (in pratica f/D è il rapporto focale F, che esprime l’apertura dello specchio).

Il raggio di Airy per uno specchio F5 per qualsiasi diametro vale perciò:

1.22 * 0.56 * 5 = 3.41 micron

Quindi per poter soddisfare al criterio di Couder, il valore dell’Aberrazione Trasversale al fuoco Atf deve essere inferiore alla unità, in quanto un Atf=1 indicherebbe il riflesso sul bordo della tacca, e un numero maggiore di 1 indicherebbe la caduta fuori di questa (individuabile anche con la posizione di quella zona che si troverebbe all’esterno della “tromba” delle tolleranze).

In effetti se il risultato fosse per una o più zone sopra l’unità, occorrerebbe procedere ad un ritocco perché lo specchio non sarebbe di buona qualità.

Il tipo di ritocco da attuare si deduce dal grafico dell’aberrazione trasversale Atf , e la quantità di vetro da togliere si deduce dal grafico con la spezzata che riproduce il profilo dell’onda. Ambedue sono il risultato del programma o foglio di calcolo utilizzato per la valutazione del test.

Al termine di ogni ritocco occorre ricalcolare il raggio R della zona centrale, e tutti i valori teorici X e Y delle varie zone, prima di iniziare un nuovo test di verifica della superficie appena corretta.

Notare che se Y misurato risulta maggiore di Y calcolato, la zona dello specchio è già troppo scavata (Alc è negativa) e siccome il “Mirror Maker” può solo asportare del vetro e non aggiungerne dove esso viene a mancare, per ritoccare quella zona occorrerà abbassare TUTTA la restante superficie dello specchio, cancellando la parabolizzazione al momento eseguita, per ritornare verso la figura sferica, in modo da poter da essa ricominciare un nuovo tentativo di parabolizzazione.

Viceversa se Y misurato è minore di Y calcolato, la zona dello specchio è troppo elevata (Alc positiva) ad indicare una zona saliente che con un ritocco può essere abbassata (togliendo vetro).

Va da sé che avvicinando con i ritocchi la nostra parabola a quella perfetta di riferimento, si riduce via via a pochi milionesimi di millimetro (nanometri), la quantità di vetro da asportare nelle ultime correzioni, e pertanto aumenta in modo esponenziale il rischio di “togliere troppo”, e quindi di dover fare un “game over” che obbliga al ritorno verso la sfera cancellando il lavoro fatto, per eseguire in seguito un nuovo tentativo di parabolizzazione.

Vale la pena di ricordare che in questi frangenti le quantità di vetro in gioco sono dell’ordine dei milionesimi di millimetro, e quindi non c’è pericolo di rovinare il proprio specchio ritornando indietro di qualche decina di essi per ritentare una nuova parabolizzazione. Il problema tutt’al più è solo quello della pazienza che bisogna mettere in gioco… per portare a termine uno specchio sicuramente eccezionale, non accontentandoci di uno specchio di qualità sicuramente superiore a quella commerciale….Ma non strepitosa.

IL BOLLETTINO DI CONTROLLO

E’ una tavola raggruppante tutti i dati di cui abbiamo scritto, che mostra i due grafici di interesse per la previsione delle correzioni.

Esso riporta i valori teorici di X e di Y; i valori pratici rilevati di Y e la differenza Ym; così come le aberrazioni longitudinale Alc e trasversale dello specchio Atf; le pendenze espresse in valore ed in segno, permetteranno così di tracciare un grafico col profilo dell’onda riflessa e di determinare la precisione sull’onda riflessa appartenente al nostro specchio (il famoso Lambda/n);

Il seguente è un esempio di bollettino di controllo su foglio di calcolo:

PRO E CONTRO DEL TEST

PRO:

1. E’ un metodo considerato impersonale perché l’arbitrio dell’osservatore interviene ben poco nelle misure
2. Le misure sono esenti da fastidiosi fenomeni di diffrazione ai bordi delle finestre di controllo

CONTRO:

1. Difficile ricerca dell’inizio della caustica, e principale fonte di errore.
2. Il compimento del test richiede più tempo del test di Foucault
3. Il tester deve possedere una precisione meccanica elevata e senza giochi delle parti in movimento.
4. Il test non fornisce dati sulla superficie, né permette di individuare un bordo ribattuto o rilevato, e difetti di dimensione inferiore alla misura delle finestre (come la rugosità) non sono percepiti.

IN CONCLUSIONE

L’utilità diffusamente riconosciuta del presente test, potrebbe sicuramente essere confortata ed arricchita da suggerimenti pratici sulla sua conduzione, che possono provenire solo dal suo utilizzo nella pratica di realizzazione di uno specchio di diametro oltre 300mm e corta focale, di non soddisfacente realizzazione col Foucault.

Questo mio, è solo un approccio conoscitivo molto superficiale. Quindi auspico che un completamento di suggerimenti possa pervenire da chiunque abbia messo il test alla prova nella pratica.