Lo sferometro

2 CommentsAmbiente e strumenti di lavoro

Lo sferometro è uno strumento di misura utilizzato nella lavorazione di uno specchio astronomico, per verificare la profondità di scavo raggiunta e quindi il raggio di curvatura della superficie in esame.
Lo strumento in sé non è complicato, esso è costituito da un struttura portante rigida su cui sono posizionati 3 piedini di appoggio disposti in modo da trovarsi ai vertici di un triangolo equilatero, mente nel centro è posizionata un dispositivo a vite o un comparatore per misurare la profondità dello scavo.

sferometro

Conoscendo la distanza radiale dei piedini dall’ astina centrale e la profondità misurata, si può, per mezzo di opportune formule matematiche, risalire al valore del raggio di curvatura della superficie.

L’astina mobile di misurazione, se di tipo a vite, è solitamente formata per l’appunto da una vite di passo 1 mm solidale con un disco graduato avente 100 divisioni, che permette quindi una lettura della misura dell’ordine del centesimo di millimetro.
I tre piedini invece, possono essere formati o da delle astine appuntite nella parte di appoggio, o da tre sferette di diametro noto. La sostanziale differenza tra le due soluzioni sta nelle diverse formule che si dovranno utilizzare per calcolare il risultato finale.

In particolare le formule da utilizzare sono:

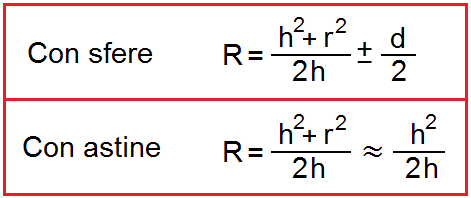
formule 2

essendo:
R = raggio di curvatura della superficie (2 volte la focale)
h = valore misurato della freccia
r = distanza radiale dei piedini dall’astina centrale
d = diametro delle sfere utilizzate

Il ± presente nella formula per il calcolo del raggio di curvatura per lo sferometro con sfere lo si deve intendere come segno + se si sta analizzando una superficie concava, mentre come segno – se si sta analizzando una superficie convessa.

Un’altra variante dello strumento è mostrata qui sotto, nella quale al posto dei tre appoggi è presente una sezione cilindrica tubolare. In questa variante se si analizza una superficie concava a poggiare su di essa sarà la corona circolare esterna, mentre se si analizza una superficie convessa a poggiare su di essa sarà la corona circolare interna. Sarà importante dunque utilizzare il corretto valore del raggio (r) nella formula, a seconda del caso in esame.

5587_2

COME UTILIZZARLO

  • La prima operazione da effettuare è verificare l’azzeramento dello strumento andando ad effettuare una misura su di una superficie perfettamente piana.

azzeramento

  • Procedere con la misurazione della superficie da analizzare.
    Se di dispone di uno sferometro con comparatore la misurazione avverrà immediatamente e senza fatica, mentre se si dispone dei uno sferometro a vite si deve agire sulla vite ruotandola per farla scendere fino a che la sua punta arrivi a contatto con la superficie.
    Le tecniche per capire quando il contatto è avvenuto sono principalmente 2:
    Nella prima, una volta che si arriva a contatto e si continua ad agire sulla vite, l’intero sferometro tenderà a ruotare su se stesso, quindi tornare leggermente indietro fino a raggiungere la posizione ideale (sensibilità 3-5 centesimi di mm); nella seconda, appena si supera anche di poco, il valore della freccia uno dei piedini si staccherà dalla superficie del vetro. Se si fa pressione alternativamente sopra i piedini di appoggio si dovrebbe sentire un ticchettio (come con un tavolo traballante), quindi tornare indietro fino alla scomparsa dell’effetto (sensibilità 1-2 centesimi di mm).

misura

  • A questo punto leggere la misura e utilizzando la formula corretta calcolare il raggio di curvatura della superficie (o la focale dividendo per 2 il risultato).
    Nell’ esempio riportato il valore della freccia è di poco più di 0.81 mm (essendo la superficie concava l’astina è scesa rispetto alla posizione di azzeramento, quindi la lancetta si è mossa in direzione antioraria).
    Applicando la formula riportata sopra, il risultato del raggio di curvatura (R) risulta pari a 920.6 mm (avendo lo sferometro in esame r=39mm e d=7.95mm).

ESEMPIO DI UNO SFEROMETRO AUTOCOSTRUITO:

Per la costruzione di questo sferometro ho utilizzato come base di supporto un ingranaggio in plastica abbastanza robusto e di diametro opportuno recuperato da una vecchia fotocopiatrice.

Ho utilizzato questo supporto perché come potete vedere dall’immagine sottostante ha un settore circolare nella arte esterna delimitato da due bordi che mi permettono di posizionare con accuratezza (almeno a livello radiale) le tre sferette di supporto in acciaio. E 12 nervature radiali che mi permettono di collocare agevolmente le sferette a 120° le une alle altre.

IMG_0269

Per bloccare in posizione il comparatore invece, è bastato praticare un foro della dimensione adeguata per permettere il passaggio dell’asta esterna del cursore che è poi stata serrata in posizione da una vite trasversale.

IMG_0275

E questo è lo sferometro competo posizionato su una superficie piana per l’azzeramento:

IMG_0265

Comments (2)

  1. deabis

    deabis

    Nella prima fase di lavodazione di uno specchio parabolico, quando si sta lavorando con una grana grossa per scavare lo specchio e raggiungere la freccia desiderata, la sfera non è per nulla perfetta. In questa fase credo sia opportuno utilizzare uno sferometro che si appoggi sul bordo dello specchio o più vicino possibile ad esso, in modo da annullare eventuali errori di misurazione dovuti ad una sfera ancora imperfetta. Ovviamente questo problema non sussiste o è minimo nelle fasi successive di lavorazione, quando, cioè, si sta lavorando con grane fini e la sfera è ormai formata.
    D’altra parte è anche vero che uno sferometro con i tre punti di appoggio (o disco di appoggio) con piccolo diametro, o comunque diametro inferiore a quello dello specchio, ci consente di fare una prima verifica della regolarità della sfera: sarà sufficiente effettuare diverse misurazioni in diversi punti dello specchio e verificare che la misura restituita dallo strumento sia costante. Contrariamente, la sfera sarà ancora imprecisa.
    Concludo dicendo che, avendo la possibilità di autocostruirsi uno sferometro, sarebbe interessante produrne almeno due, uno con appoggi sufficientemente ampi da posizionarsi sul bordo dello specchio ed uno con appoggi più “stretti”: in questo modo avrò due strumenti utili in due diverse fasi di lavorazione, che ci consentiranno anche di confrontare e quindi di verificare le misurazioni nelle fasi avanzate di lavorazione.

  2. Giulio Tiberini

    Bisogna tenere comunque presente che lo sferometro è utile solo quando si abbia una qualche garanzia che la superficie curva da misurare sia oggettivamente almeno uno sferoide uniforme, altrimenti non c’è nessuna garanzia che quella misurata sia realmente una superficie sferica.

    Infatti la rilevazione del raggio di curvatura appartenente alla sfera incognita che collega il punto di misura centrale dello sferometro, con il diametro del piano individuato dai suoi tre piedini periferici, è esatta solo se la superficie fra i punti di misura è sferica.

    Dal punto di vista del “fai da te” dell’astrofilo che realizza il proprio specchio a mano libera, lo sferometro non è necessario, perchè l’unica garanzia che la curva prodotta dal lavoro manuale sia un buon sferoide, è data dalla scomparsa della bolla d’aria persistente dopo la sbozzatura perchè intrappolata fra lo specchio e l’utensile.
    Infatti fino a che la bolla di aria è presente, è segno che le due superfici specchio e utensile non hanno lo stesso raggio di curvatura.

    Secondo i consigli di dello stesso Foucault (che fu il fautore della realizzabilità manuale di specchi in vetro, in una epoca in cui sembrava possibile realizzarli solo in metallo), per arrivare sicuramente ad una buona sfera, occorre mettere in pratica solo le 5 regole seguenti:
    – Utilizzare un utensile a pieno diametro;
    – Avere l’accortezza di applicare delle corse di ampiezza nel senso avanti-indietro di 1/3 Diametro, “centro su centro” (quindi con debordo avanti-indietro di 1/6 del diametro specchio);
    – Badando contemporaneamente di rimanere centrati con tali corse nel senso destra-sinistra, cioè senza debordare lateralmente (Perchè il debordo laterale porterebbe a svasare troppo precocemente la sfera verso la parabola, quando essa ancora non è perfettamente lucida; Oppure a produrre una superficie svasata oltre la parabola).
    – Infine occorre lavorare ruotando a piccoli passi attorno al tavolo,
    – ruotando pure di un poco alla volta nel senso opposto, il vetro che si ha in mano.
    Ed è tutto.

    Vista la grande quantità di corse che unitariamente asportano pochissimo vetro, è la statistica dei grandi numeri che applicando un comportamento simile, produce buone superfici sferiche raggiungendo grandissima precisione di lavorazione anche a mano libera, poichè i piccoli errori di segno opposto si elidono a vicenda.

Leave a comment