- Este tema tiene 98 respuestas, 3 voces, y se actualizó por última vez 7 años, 12 meses hace por
.
-
Mensajes
-
Si exacto Massimo, Estoy de acuerdo con todo excepto que la inclinación es necesaria, de hecho en el artículo que vinculó desde Northek, más o menos un 3/4 de la página (justo encima del capítulo “flecos elípticos”) en la imagen con el 3 diferentes tipos de formas marginales que se pueden ver, el de la izquierda se refiere precisamente a una situación sin inclinación.
Para estimar el valor del PV, de hecho, se hace como usted dice, y se explica más en la página 13 dell’ Prueba de taller óptico.
Sin embargo, siempre hay artículos interesantes sobre Northek…Con el tiempo, casi todos me han sido leídos…
y, Dije eso mal, Quise decir sin una capa de separación, con “inclinación” significa una capa de separación no uniforme, entonces “inclinado”, derecho ?
también porque, si pongo dos superficies iguales ( o casi ) en contacto sin ninguna separación, no hay riesgo de “unión” o al menos un fuerte efecto de succión ?
Sí, inclinación exacta = inclinación y también es cierto, ya que dice que si pone en contacto dos superficies extremadamente precisas y una negativa, la otra formaría un fuerte efecto de succión…
Ok mirco, gracias
Mientras tanto, he llegado a una buena 70% de pulido, la forma no parece cambiar y, por lo tanto, no creo que lo complete todo antes de comenzar la hipérbola, también porque con el tiempo que tomará llegar a K = -5.12, yo (el?
) hoyos residuales / e serán un recuerdo lejano… 
Más bien me preguntaba cómo se verifica el estado de rugosidad….
También por este motivo e, no confiar demasiado en mis habilidades con interferometría ( aunque tan simple como la de Newton ) Estoy montando la versión telescopio “prototipo” es decir, con los componentes de madera obtenidos del antiguo Dobson adaptados al nuevo proyecto.
Verificaciones y verificaciones de pruebas realizadas en “garaje”, Me gustaría apoyarlos con aquellos hechos directamente en el cielo, con la ayuda de la prueba de estrellas y la buena cuadrícula de Ronchi, ellos a diferencia de mi, apenas se equivocan…
supongo, pero creo que de manera cualitativa trataría de ver la aspereza del plan con Foucault, como se hace con espejos esféricos o parabólicos, pero en este caso insertando el plano en la trayectoria óptica de un primario no rugoso, como si fuera un secundario de 45 °, y luego colocando el probador de Foucault en el costado aproximadamente a la distancia del radio de curvatura para ver el primario reflejado desde el plano.
iluminaría, luego mueva un poco la orientación de la fuente para que la iluminación sea menos brillante, que normalmente resalta inmediatamente la rugosidad de la superficie (o el polvo o la suciedad infinitesimal) que aparecería tan usual como nubes claras.
supongo, pero creo que de manera cualitativa trataría de ver la aspereza del plan con Foucault, como se hace con espejos esféricos o parabólicos…
Giulio, no tienes que decirme estas cosas, porque entonces realmente los hago !
Dado que estas franjas de Newton no me convencen en absoluto, ciertamente no por la validez de la prueba sino por cómo lo estoy haciendo de esta manera… aproximado, entonces me dije:
Okay, no podemos probar la superficie convexa por razones obvias, mamá…. si ponemos el espejo en el banco de pruebas ronchi / foucault al contrario , Qué pasa ?
Definitivamente la parte convexa, visto desde este otro lado se vuelve cóncavo con reflejos convergentes, los problemas están representados por la capa de vidrio que es cruzada dos veces por la luz, y la superficie plana ( que en este caso se convierte en el frontal ) que ciertamente no es plano…
– la superficie plana no contribuye a los reflejos ni a la refracción, en caso de que la no planaridad altere la regularidad de la capa de vidrio y, por lo tanto, la intensidad local de la refracción que, tal como lo conocemos, contribuye juntos a la curvatura del vidrio para determinar la distancia focal o, mejor decir ya que estamos usando vidrio como lente, de potencia dioptrica.
pero cuánto puede variar la refracción real con una forma “casi plano” que un piso ? Yo no sé, por el momento vamos a ver que pasa
Mientras tanto, descubrí algo fundamental : mi led no es monocromático
Una pena! 
entonces una primera medida que será útil: el radio de curvatura (774 mm ), con el aporte de doble refracción de vidrio, lleva el plano focal a la distancia de 510 mm , por lo tanto más corto, como se esperaba.
Imágenes de Ronchi “poco convencional” en cambio nos dicen que la superficie no sería esférica, pero con la periferia creciendo con respecto al centro ( somos intra-focales ), sin embargo, la tendencia es muy regular y simétrica., lo que nuevamente me hace pensar que el “cara casi plana” afecta imperceptiblemente en esta reflexión-refracción.
Pero recordemos que estamos mirando la supuesta esfera desde adentro, por lo tanto, la superficie del espejo convexo debe estar con la periferia inferior y el centro superior de lo necesario, Estás de acuerdo ?
la madre de todas las preguntas en este punto sería: la forma de la superficie reflectante es realmente así, o es alterado por la doble refracción de manera irregular, es decir, hacer que la esfera parezca una esfera achatada ?
Una primera pista me viene del hecho de que el centro llega un poco tarde con el esmalte, así que en realidad podría ser “Alto” porque menos logrado por el procesamiento, pero vamos más allá y veamos el tema de “prueba”: aspereza
Ajustamos la cámara web en escala de grises para evitar colores engañosos, aumente ligeramente el contraste e intente usar la cuchilla Foucault:
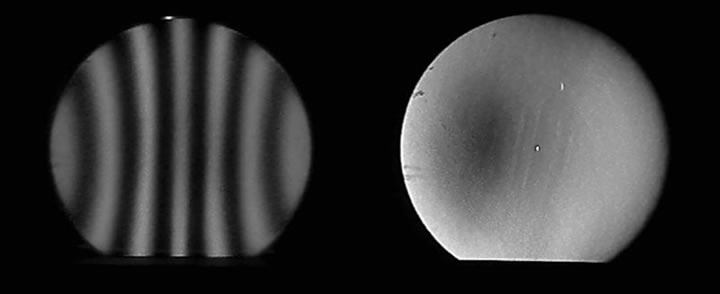
Y aquí estamos con la imagen clásica., Lo hicimos, la aspereza está ahí y se nota !
Análisis
: El punto luminoso central es el reflejo de la fuente en la cara plana, el “Manchas solares” son defectos de cara sucia / plana, todo lo demás, creo, está realmente allí “nubes claras” que Giulio dijo , las irregularidades de la superficie reflectante. Que niño ?hola Massimo, sí, también hice las pruebas de Ronchi “en el reverso” y en realidad debido a la doble refracción, el radio de curvatura del espejo también se vuelve mucho más pequeño para mí…
Además creo (Corrígeme si estoy equivocado) que la prueba de Ronchi en este caso debe leerse al revés, en el sentido de que lo que vemos ahora en la posición intrafocal, sería lo que veremos en una posición extrafocal en una prueba clásica en una superficie cóncava…Es decir, si vi líneas rectas que, sin embargo, cerca del borde, se tiran todas (intrafocale) Yo diría que he elevado el borde, y es verdad si miro la superficie desde este lado, pero si volteo el espejo y lo miro desde el lado que luego debería convertirse en el reflector, ese borde elevado debería convertirse en un borde remachado (por complementariedad)…
Lo que me gustaria hacer, si tengo tiempo en el futuro cercano, es calcular cuál debe ser la forma de las líneas de Ronchi en presencia de ambas superficies perfectas, luego el frente plano y el trasero perfectamente esférico. Para entender si la doble refracción afecta o no los resultados de la prueba…bien, Mientras tanto, he llegado a la conclusión de que la doble refracción no afecta la forma de las líneas de Ronchi
como digo esto ?la primera refracción, es decir, la entrada de la fuente de luz hasta la parte cóncava reflectante, simplemente no está allí,
1-la refracción ocurre solo en presencia de superficies curvas ( dioptrías ) que separan dos materiales con diferentes índices de refracción. En el caso de una superficie plana, en cuanto a las lentes, no hay desviación del haz de luz. Si la superficie no era plana sino esférica con un radio de curvatura muy largo, asimismo, ofrecería una contribución mínima e imperceptible tanto a la distancia focal general como a la forma de las líneas.
2- incluso en interferometría hay una doble refracción, pero el primer 'cruce de luz en la superficie plana se considera irrelevante.
3-Descubrí que alguien mucho más experimentado que yo usa este método para probar la forma de los secundarios en cassegrains ( pecado, Esperaba haberlo inventado
):
http://www.oldhamoptical.com/#!convex-surfaces/ctxndijo esto, llegamos a lo que dijiste Mirco, en las líneas de Ronchi.
1-No tenemos que preocuparnos de cómo se verían las líneas de Ronchi en la superficie convexa porque simplemente no estarían allí. La prueba de Ronchi, cómo la superficie bajo examen es única, la forma detectada es la misma desde donde se mire, solo cambia la dirección de la curvatura creciente o decreciente, que se vuelve opuesto y complementario, en otras palabras, qué en el lado convexo “crecer”, en el lado cóncavo “disminuye” y viceversa.
2-mi’ solo tenemos que razonar en el lado opuesto de la superficie, pero no por la forma de las líneas, pero para las técnicas de procesamiento que deben pensarse de otra manera, explicaré mejor:
como bien dijiste, el borde elevado visto desde el lado convexo se remacha ( inversión de la tendencia de curvatura, como dijimos en el punto 1 )
Esto significa que si estamos trabajando como una superficie cóncava normalmente se hace, implementaremos técnicas para quitar el vidrio en los lugares correctos para obtener la forma correcta.
Mirando al otro lado, es decir, tener que intervenir en la superficie convexa, tenemos que corregir el mismo error ( con respecto a la misma superficie de referencia, ad es. la esfera ), pero no podemos hacerlo con la técnica que hubiéramos usado en el espejo cóncavo, porque, en este otro lado del espejo, significaría tener que agregar algo de material.
Entonces, tenemos que trasladar la esfera de referencia hacia arriba para llevar el borde dentro del volumen que se está procesando para ver el vidrio que se eliminará en la superficie convexa, para llegar a la misma forma.
seguro, lo que tenemos que pensar “al contrario”, son los errores, como ya adivinaste:
la “agujero central” en el cóncavo ( nosotros en Ronchi solo vemos esta perspectiva ), se convierte “Collina” en el convexo:
corrección: cavas centralmente en el convexo, exactamente lo contrario de lo que habríamos hecho en el cóncavo.el anillo levantado en el cóncavo , se deprime sector en el convexo
el borde remachado en el cóncavo, se convierte en borde elevado en el convexopero en todos estos casos la forma es idéntica, solo cambia el punto de vista y la posibilidad de quitar el vidrio, y luego llegamos a “primer postulado” ( el teorema ?
) por massimar 
Analizando la superficie del espejo desde la parte cóncava, correcciones de forma en la parte convexa, deben ser pensados “contrario”, es decir, utilizando la técnica que en la parte cóncava habría generado los errores que queremos corregir.
Ya he experimentado todo esto en el espejo, luego tomo fotos y publico los resultados.
Ponerse de acuerdo sobre todo…
Sin embargo, estoy haciendo un pequeño programa para verificar que las líneas de Ronchi no se desvíen de la doble refracción…No es que no confíe en tus palabras, pero sabes que si no meto la nariz no soy feliz…
derecho !
También sería interesante encontrar la relación que vincula la segunda refracción con el punto focal de reflexión., quizás a partir de las fórmulas conocidas para calcular la distancia focal de las lentes, mientras que el índice de refracción del vidrio de calcio-sodio es 1,52.entonces, cálculos preliminares realizados…
Por lo que veo, las líneas de Ronchi para una esfera perfecta deberían verse en (intrafocale) como las que verías para una parábola extrafocal. En realidad, no serían exactamente idénticos a los de una parábola perfecta., pero serían muy diferentes, tanto que prácticamente no notaremos la diferencia…
Usando sus fotos y haciendo una comparación con el software de simulación Ronchi, se ve tan bien como su superficie, que está cerca de una esfera (al menos según las imágenes de las franjas de difracción) son similares a los de una parábola…Como también muestran los cálculos… Además los cálculos me dicen que para tu espejo, debido a la doble refracción, el centro de curvatura “alterado” estaría en 512.5 mm de la superficie bajo examen… Con excelente correspondencia con el valor que encontraste…
Mirco eres un genio ! ahora espero que me expliques paso a paso, porque todavía no entiendo cómo diablos lo hiciste, cómo la refracción en la reflexión interfiere y se calcula.
Bueno genio, no exageremos…
No sé si podré explicarlo bien, Pero lo intento…Me ayudo con un dibujo:
Esto en palabras, y esto en fórmulas:
Sin embargo, para el programa en Excel que muestra la imagen real de la prueba, tendrá que esperar porque no es tan fácil de implementar…eh eh…
Gran mirco ! ahí es donde me equivoqué, en la primera refracción ( y también en el segundo ) Pensé en vigas paralelas ( yo ya estaba “acecho” las estrellas
), pero, por supuesto, se debe considerar el ángulo de ataque !Si en cambio consideramos una fuente hasta el infinito, no tendremos la primera refracción ( θ1 = 0 ) para cada valor de B , entonces cuando B tiende a 0, es decir, acercarse al eje óptico, también las segundas refracciones tenderán a cero y por lo tanto nunca habrá refracciones para los rayos axiales.
Qué significa eso ? que en este caso, el plano focal para una fuente infinita es un cáustico, con el vértice equivalente al de un espejo con el mismo radio de curvatura pero sin vidrio reflectante en el frente ?
Otra consideración, leyendo tus cálculos;
uno podría relacionar L con Xrit ( y por lo tanto también los ángulos θ1 y θ4 ) ya que hay un punto donde L y X toman el mismo valor y es exactamente lo que usamos para la fuente y la prueba de red en el “presunto” plano focal.Digo esto porque podría ser un método, luego usando el procedimiento inverso, calcular el radio de curvatura del espejo convexo conociendo la medida de la distancia de la fuente.
- Usted debe ser conectado para responder a este tema.