- Questo topic ha 98 risposte, 3 partecipanti ed è stato aggiornato l'ultima volta 7 anni, 3 mesi fa da
.
-
Post
-
Si esatto Massimo, concordo su tutto a parte sul fatto che che il tilt sia necessario, infatti sull’articolo che hai linkato di Northek, più o meno a 3/4 della pagina (appena sopra il capitoletto “frange ellittiche”) nell’immagine con le 3 diverse tipologie di forme delle frange che si possono vedere, quella più a sinistra si riferisce proprio ad una situazione senza tilt.
Per stimare il valore del PV in effetti si fa come dici tu, ed è in oltre spiegato più estesamente alla pagina 13 dell’ Optical shop testing.
Comunque sempre interessanti gli articolo su Northek…Nel tempo me li sono letti quasi tutti…
Si, mi sono espresso male, intendevo senza uno strato di separazione, con “tilt” si intende uno strato di separazione non uniforme, quindi “inclinato”, giusto ?
Anche perché, se metto due superfici uguali ( o quasi ) a contatto senza nessuna separazione, non c’è il rischio di “incollaggio” o quantomeno di un forte effetto ventosa ?
Si esatto Tilt = inclinato ed è anche vero come dici tu che se poni a contatto due superfici estremamente precise e una il negativo dell’altra si formerebbe un forte effetto ventosa…
Ok Mirco, grazie
Nel frattempo sono arrivato a un buon 70% della lucidatura, la forma non sembra cambiare e perciò non penso che la completerò tutta prima di iniziare l’iperbole, anche perchè con il tempo che ci vorrà per arrivare a K=-5.12, i (le?
) pits residui/e saranno un lontano ricordo… 
Piuttosto mi chiedevo come si fa a controllare lo stato della rugosità….
Anche per questo motivo e, non fidandomi più di tanto con le mie capacità con l’interferometria ( anche se semplice come questa di Newton ) sto assemblando il telescopio in versione “prototipo” cioè con i componenti in legno ricavati dal vecchio Dobson adattati al nuovo progetto.
I controlli e le verifiche dei test fatti in “garage”, vorrei supportarli con quelli fatti direttamente sul cielo, con l’aiuto dello star test e del buon vecchio reticolo di Ronchi, loro al contrario di me, difficilmente si sbagliano…
Tiro a indovinare, ma credo che in modo qualitativo tenterei di vedere la rugosità del piano con Foucault, come si fa con gli specchi sferici o parabolici, ma in questo caso inserendo il piano nel percorso ottico di un primario non rugoso, come se si trattasse di un secondario a 45°, e quindi piazzando di lato il tester di Foucault all’incirca alla distanza del raggio di curvatura per vedere il primario riflesso dal piano.
Illuminerei, per poi manovrare un poco l’orientamento della sorgente per rendere l’illuminazione meno brillante, la qual cosa normalmente mette subito in risalto la rugosità superficiale (o la infinitesima polvere o sporcizia) che si presenterebbe come al solito come nuvolette chiare.
Tiro a indovinare, ma credo che in modo qualitativo tenterei di vedere la rugosità del piano con Foucault, come si fa con gli specchi sferici o parabolici…
Giulio, non devi dirmi queste cose, perché poi io le faccio davvero !
Dato che queste frange di Newton non mi convincono per niente, non certo per la validità del test ma per come lo sto facendo io in modo così… approssimato, allora mi sono detto:
Ok, non possiamo testare la superficie convessa per ovvi motivi, ma…. se mettiamo lo specchio sul supporto per il test ronchi/foucault al contrario , cosa succede ?
Sicuramente la parte convessa, vista da quest’altro lato diventa concava con le riflessioni convergenti, il problemi sono rappresentati dallo strato di vetro che viene attraversato due volte dalla luce, e la superficie piana ( che in questo caso diventa quella frontale ) che sicuramente piana non è…
– la superficie piana non contribuisce alle riflessioni e neanche alla rifrazione, casomai la non planarità altera la regolarità dello strato di vetro e quindi l’intensità locale della rifrazione la quale, come sappiamo, contribuisce insieme alla curvatura del vetro alla determinazione della lunghezza focale o, per meglio dire visto che stiamo usando il vetro come una lente, del potere diottrico.
ma quanto poi potrà variare l’effettiva rifrazione con una forma “quasi piana” rispetto a una piana ? non lo so, per il momento andiamo a vedere che succede
Intanto ho scoperto una cosa fondamentale : il mio led non è monocromatico
un vero peccato! 
poi una prima misura che potrà tornarci utile: il raggio di curvatura (774 mm ), con il contributo della doppia rifrazione del vetro, porta il piano focale alla distanza di 510 mm , quindi più corto, come era prevedibile.
Le immagini del Ronchi “anticonvenzionale” ci dicono invece che la superficie non sarebbe sferica, ma con la periferia crescente rispetto al centro ( siamo in intra-focale ), tuttavia l’andamento è molto regolare e simmetrico, il che mi fa nuovamente pensare che la “faccia quasi-piana” influisce in modo impercettibile in questa riflessione-rifrazione.
Ricordiamoci però che stiamo guardando la presunta sfera dall’interno, quindi la superficie dello specchio convesso dovrebbe essere con la periferia più bassa e centro più alto del dovuto, siete d’accordo ?
la madre di tutte le domande a questo punto sarebbe: la forma della superficie riflettente è realmente così, o viene alterata dalla doppia rifrazione in modo irregolare, portando cioè la sfera a sembrare una sfera oblata ?
Un primo indizio mi viene da fatto che il centro è leggermente in ritardo con il lucido, quindi potrebbe effettivamente essere “alto” perché meno raggiunto dalla lavorazione, ma andiamo oltre e veniamo all’argomento del “test”: la rugosità
Regoliamo la web-cam in scala di grigio per evitare colori fuorvianti, aumentiamo leggermente il contrasto e proviamo ad utilizzare la lama di Foucault:
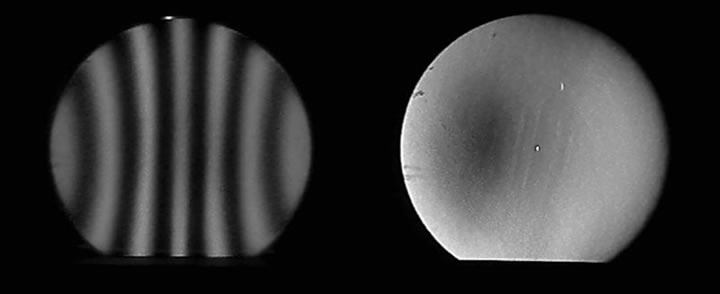
Ed eccoci alla immagine classica, ce l’abbiamo fatta, la rugosità c’è e si vede !
Analisi
: il punto luminoso centrale è il riflesso della sorgente sulla faccia piana, le “macchie solari” sono sporco/difetti della faccia piana, tutto il resto io credo siano effettivamente le “nuvolette chiare” che diceva Giulio , le irregolarità della superficie riflettente. Che ne dite ?Ciao Massimo, si anche io ho effettuo i test di Ronchi “al rovescio” ed effettivamente a causa della doppia rifrazione anche a me il raggio di curvatura dello specchio diventa molto più piccolo…
In oltre penso (correggetemi se sbaglio) che il test di Ronchi in questo caso è da leggersi al contrario, nel senso che quello che vediamo in posizione intrafocale ora, sarebbe quello che vedremo in posizione extrafocale in un test classico su di una superficie concava…Ovvero se vedessi delle linee dritte che però in prossimità del bordo si buttano tutte all’esterno (intrafocale) mi verrebbe da dire che ho bordo rialzato, ed è vero se guardo la superficie da questa parte, ma se capovolgo lo specchio e lo guardo dal lato che poi dovrebbe diventare quello riflettente quel bordo rialzato dovrebbe trasformarsi in bordo ribattuto (per complementarità)…
Quello che mi piacerebbe fare, se prossimamente avrò del tempo, è di calcolare quale dovrebbe essere la forma delle linee del Ronchi in presenza di entrambe le superfici perfette, quindi quella anteriore piana e quella posteriore perfettamente sferica. In modo da capire se la doppia rifrazione influisce o meno sui risultati del test…Bene, intanto sono arrivato alla conclusione che la doppia rifrazione non influisce sulla forma delle linee del Ronchi
come faccio a dire questo ?la prima rifrazione, cioè l’ingresso della luce-sorgente fino alla parte concava riflettente, semplicemente non c’è,
1-la rifrazione avviene solo in presenza di superfici curve ( diottri ) che separano due materiali con indici di rifrazione diversi. Nel caso di una superficie piana, come per le lenti, non c’è deviazione del fascio luminoso. Nel caso invece che la superficie non fosse piana ma sferica con raggio di curvatura lunghissimo, analogamente offrirebbe un contributo minimo ed impercettibile sia alla focale complessiva che alla forma delle linee.
2- anche nell’interferometria c’è una doppia rifrazione, ma viene considerato ininfluente il primo ‘attraversamento della luce sulla superficie piana.
3-Ho scoperto che qualcuno molto più esperto di me utilizza questo metodo per testare la forma dei secondari nei cassegrain ( peccato, speravo di averlo inventato io
):
http://www.oldhamoptical.com/#!convex-surfaces/ctxndetto questo, veniamo a quello che dicevi tu Mirco, sulle linee del Ronchi.
1-Non dobbiamo preoccuparci di come sarebbero le linee del Ronchi sulla superficie convessa perchè semplicemente non ci sarebbero. Il Test di Ronchi, come la superficie in esame è univoco, la forma rilevata è la stessa da qualunque parte si guardi, cambia solo il senso di curvatura crescente o decrescente, che diventa opposto e complementare, in altre parole ciò che dal lato convesso “cresce”, dal lato concavo “decresce” e viceversa.
2-E’ giusto invece che dobbiamo ragionare sulla parte opposta della superficie, ma non per la forma delle linee, ma per le tecniche di lavorazione che vanno pensate al contrario mi spiego meglio:
come hai giustamente detto, il bordo rialzato visto dalla parte convessa diventa ribattuto ( inversione dell’andamento della curvatura, come dicevamo al punto 1 )
questo significa che se stiamo lavorando come si fa normalmente una superficie concava, metteremo in atto delle tecniche per togliere il vetro nei punti giusti per arrivare alla forma corretta.
Guardando dall’altro lato, dovendo cioè intervenire sulla superficie convessa, dobbiamo correggere lo stesso errore ( rispetto ad una medesima superficie di riferimento, ad es. la sfera ), ma non possiamo farlo con la tecnica che avremmo usato nello specchio concavo, perchè, da quest’altra parte dello specchio, significherebbe dover aggiungere del materiale.
Quindi dobbiamo traslare la sfera di riferimento fino a portare il bordo all’interno del volume in lavorazione per vedere il vetro da togliere sulla superficie convessa, per arrivare alla medesima forma.
in definitiva, quello che dobbiamo pensare “al contrario”, sono gli errori, come già avevi intuito tu:
il “buco centrale” nel concavo ( noi nel ronchi vediamo solo questa prospettiva ), diventa “collina” nel convesso:
correzione: si scava centralmente nel convesso, esattamente il contrario di quello che avremmo fatto nel concavo.l’anello rialzato nel concavo , diventa settore depresso nel convesso
il bordo ribattuto nel concavo, diventa bordo rialzato nel convessoma in tutti questi casi la forma è identica, cambia solo il punto di vista e la possibilità di togliere il vetro, e quindi arriviamo al “primo postulato” ( o teorema ?
) di massimar 
Analizzando la superficie dello specchio dalla parte concava, le correzioni di forma sulla parte convessa, vanno pensate al “contrario”, utilizzando cioè la tecnica che sulla parte concava avrebbe generato gli errori che vogliamo correggere.
ho già sperimentato tutto questo sullo specchio, più tardi faccio delle foto e posto i risultati.
D’accordo su tutto…
Io comunque mi sto facendo un programmino per verificare che le linee del Ronchi non subiscano deviazioni dalla doppia rifrazione…Non che non mi fidi delle tue parole, ma sai se non ci metto il naso non sono contento…
Giusto !
sarebbe interessante anche trovare la relazione che lega la seconda rifrazione alla focale della riflessione, magari partendo dalle formule note per il calcolo della focale delle lenti, considerando che l’indice di rifrazione del vetro calcio-sodico è di 1,52.Allora, calcoli preliminari fatti…
Da quel che vedo le linee del Ronchi per una sfera perfetta dovrebbero vedersi in (intrafocale) come quelle che si vedrebbero per una parabola in extrafocale. In realtà non sarebbero proprio identiche a quelle di una parabola perfetta, ma sarebbero leggerissimamente diverse, tanto che praticamente non ci accorgeremo della differenza…
Utilizzando le tue foto e facendo un confronto alla buona con un software di simulazioni del Ronchi si vede bene come la tua superficie, che è prossima ad una sfera (almeno stando alle immagini delle frange di diffrazione) sono simili a quelle di una parabola…Come dimostrano anche i calcoli del resto… In più i calcoli mi dicono che per il tuo specchio, a causa della doppia rifrazione, il centro di curvatura “alterato” si troverebbe a 512.5 mm dalla superficie in esame… Con ottima corrispondenza con il valore che hai trovato tu…
Mirco sei un genio ! ora mi aspetto che mi spieghi passo-passo, perchè non ho ancora capito come diavolo hai fatto, come interferisce e si calcola la rifrazione nella riflessione.
Beh genio, non esageriamo…
Non so se sarò in grado di spiegarlo bene, ma ci provo…mi aiuto con un disegno:
Questo a parole, e questo a formule:
Per il programmino in Excel che mostri l’immagine vera e propria del test però dovrai aspettare perchè non è poi così semplice da implementare…eh eh…
Grande Mirco ! ecco dove mi sbagliavo, sulla prima rifrazione ( e anche sulla seconda ) pensavo a raggi paralleli ( stavo già “guardando” le stelle
), ma ovviamente va considerato l’angolo di incidenza !Se invece consideriamo una sorgente all’infinito, non avremo la prima rifrazione ( θ1=0 ) per ogni valore di B , quando poi B tende a 0, avvicinandoci cioè all’asse ottico, anche le seconde rifrazioni tenderanno a zero e quindi non ci saranno mai rifrazioni per i raggi assiali.
Cosa significa ? che in questo caso, il piano focale per una sorgente all’infinito è una caustica, con il vertice equivalente a quello di uno specchio con lo stesso raggio di curvatura ma senza vetro rifrangente davanti ?
Altra considerazione, leggendo i tuoi calcoli;
si potrebbe mettere in relazione L con Xrit ( e quindi anche gli angoli θ1 e θ4 ) in quanto esiste un punto in cui L e X assumono lo stesso valore ed è proprio quello che abbiamo utilizzato per il test con sorgente e reticolo sul “presunto” piano focale.Lo dico perché potrebbe essere un metodo, utilizzando poi il procedimento inverso, per calcolare il raggio di curvatura dello specchio convesso conoscendo la misura della distanza della sorgente.
- Devi essere connesso per rispondere a questo topic.