- Questo topic ha 142 risposte, 6 partecipanti ed è stato aggiornato l'ultima volta 9 anni, 2 mesi fa da
.
-
Post
-
Mah, ho i miei dubbi…
ho provato a cambiare la maschera, a utilizzare diverse fenditure con diversi materiali, ( anche un foro stenopeico ), mettendo perfettamente al centro dell’oculare la singola fenditura ma il risultato non cambia:
C’è sempre una zona longitudinale di circa due millimetri in cui l’immagine sembra nel “miglior fuoco”, e spostandosi all’interno di questo intervallo non si percepisce alcuna differenza.
Mi sono chiesto quale sia la causa e credo di averla trovata.
mi ha fatto riflettere una cosa che ha detto Giulio:“Per questo motivo mi sarebbe piaciuto avere al posto del capello di Mirco, un “Ave Maria” …oppure il testo dell” internazionale” scritti in microfilm, da poter riuscire a leggere almeno una parola per poterlo considerare sufficientemente a fuoco.”ho infatti provato a utilizzare una sorgente-fenditura con quanti più dettagli fini possibili pensando che, più sono fini i dettagli maggiore sarà la certezza del punto di fuoco.
guardate questa immagine:
quello che si vede è una striscia larga 1 mm di un cartoncino ritagliato con delle forbici posizionato sul diaframma di campo dell’oculare. Sono ben visibili i “filamenti” delle fibre del cartoncino residui del taglio con forbici. il loro spessore è sicuramente dell’ordine dei centesimi di mm.
Ho realizzato una fenditura per il led, avvicinando due striscette di cartoncino ritagliate come quella in foto, e mi aspettavo di poter vedere i filamenti durante la messa a fuoco, ma niente da fare… di filamenti nemmeno l’ombra, anzi i bordi della fenditura sembravano netti come quelli della fenditura con le lame.
A questo punto sono sicuro che avrete già capito quale è il problema
partiamo da una semplice calcolo:
il potere risolutivo di uno specchio/foro di 15 mm è di 9 secondi d’arco , secondo la nota formula, R”=135/D
alla distanza di 1500 mm , 9 secondi d’arco sono l’angolo sotto il quale viene visto un oggetto di 0,07 mmquesto non significa che gli oggetti uguali o più piccoli di questa dimensione non saranno visibili, ma che vedremo solamente la loro figura di diffrazione, se poi gli oggetti saranno “abbastanza” più piccoli ( come nel caso dei filamenti di carta ) non li vedremo affatto.
Le dimensioni di alcune delle fenditure che ho utilizzato sono paragonabili al potere risolutivo del foro di 15 mm, mentre per quelle più grandi ho sempre cercato di mettere a fuoco i dettagli fini i quali non erano visibili se non nella loro figura di diffrazione. ( ed inoltre nel mio “laboratorio” in questi giorni di finestre spalancate c’è un pessimo seeing
)Vacca! Non avevo pensato al potere risolvente……
.E però mi viene in mente che l’immagine della fenditura si dice che non sia direttamente fruibile alla retina del nostro occhio, con o senza oculare che la guarda riflessa dallo specchio durante il Foucault. Se è così e non sto prendendo un granchio, mi parrebbe che una soluzione potrebbe venire nel “rovesciare la frittata”, non cercando di vedere quell’oggetto a fuoco attraverso l’oculare, ma di metterlo a fuoco su un piccolo scherno plastico trasparente da installare dove ora si trova il diaframma di campo dell’oculare del test, simulando quel che succede su una lente quando si regola il parallelismo coltello-fenditura.
Tutt’al più occorrerebbe usare un oculare o la webcam per ingrandire quella minuscola immagine.
————————————-
AGGIUNTA SUCCESSIVA: Mi rendo conto ragionando a “ruota libera” che ho effettivamente preso un granchio.
Infatti con un oculare si deve rendere visibile la immagine della fenditura (o di una stella all’infinito attraverso un telescopio) nel punto focale del sistema, nel quale si deve venire a trovare il diaframma di campo dell’oculare.Un altro ragionamento mi porta a pensare che sia effettivamente un problema l’identificazione certa della prima zona come punto di partenza, l’unica che giace sull’asse pttico, per calcolare dove dovrebbero trovarsi le distanze X delle altre zone corrispondenti ai centri dei fori della maschera.
Tant’è che Lecleire suggerisce di usare appunto quella specie di maschera di hartmann a tre fori per concludere che la zona 1 si raggiunge quando le due immagini fornite dalle aperture periferiche della maschera, col movimento longitudinale del carrello del tester, si sovrappongono alla immagine proveniente dal foro centrale. Nel caso tuo che hai un foro centrale nello specchio, le due immagini periferiche forse devono sovrapporsi alle due immagini fornire dalle due finestre centrali delle tue due prime zone che stanno a cavallo del centro forato dello specchio.
la maschera a tre fori mi sembrava fosse più che altro per l’allineamento del carrello con l’asse ottico… mi era sfuggita questa parte
In ogni caso il problema è su tutte le zone, periferiche o centrali. Il “miglior fuoco” è spalmato in un intervallo di un paio di millimetri, per il livello di precisione richiesta sono un’enormità…
mah…qui ci vuole una birretta a rinfrescarmi le idee
Si infatti, ricapitolando le operazioni del test (da quanto ho capito) io farei così:
Una volta ben allineato all’asse ottico il tester della caustica, con l’uso di una maschera tipo Hartmann a 4 finestre (due finestre periferiche della maschera che facciano coppia con le altre due finestre coincidenti con il centro di curvatura della prima zona utile, vicino al foro centrale dello specchio)……Maschera a 4 finestre che io riterrei valida per gli specchi che al centro presentano un foro (e dico ciò come estensione del principio descritto da Lecleire che riguarda una maschera con tre sole finestre, una centrale e due periferiche, idonea per specchi non forati al centro);
Cercherei la Punta della caustica, ma al posto di utilizzare il mio metodo (descritto nella pratica del mio test di Foucault) per trovare quello stesso luogo che sta al centro di curvatura delle due zone centrali, ed è l’unico GIACENTE sull’asse ottico, utilizzerei il metodo ( …a mia insaputa molto simile al mio….) suggerito da Lecleire, che (pur non comprendendolo io bene a fondo, e che verificherei in pratica per convincermi) dice di…
Piazzare la maschera di Couder e chiudere tutte le finestre ad eccezione del paio posto ad h=0.5 ed utilizzare Foucault per spostare il carro longitudinale fino a vedere all’oculare la sovrapposizione delle due immagini della fenditura in una sola immagine (anche se essa non può essere bene a fuoco) nel punto coincidente con il punto detto P, dove il test di Foucault si aspetterebbe di trovare la tinta piatta sull’asse ottico, e rilevare la misura del tiraggio…che immaginiamo per esempio sia 12mm.
Conoscendo il tiraggio della zona misurato col Foucault (e Lecleire dice che se lo specchio in esame si trova già al valore di almeno Lambda/4, si può benissimo prendere per buono il valore teorico hm^2/R…che per esempio immaginiamo sia 10mm)…
Se la sorgente fenditura sono solidali all’oculare, il centro di curvatura esatto della zona centrale dello specchio, cioè della caustica, si trova a 12-(10/2)=7mm dalla origine della vite micrometrica.Messo il tester in quella posizione, installerei la maschera della caustica e con l’applicazione delle formule relative alla equazione della parabola di riferimento, troverei un numero di valori di spostamento teorico longitudinale X , di tante posizioni quante sono le zone ada misurare.
Ad ognuno dei valori delle X teoriche devo sommare il tiraggio di posizione nel punto dove si trova LA PUNTA della caustica, per trovare i valori reali di spostamento in X che portino il mio carrello longitudinale di volta in volta alle varie distanze X teoriche determinate dalla parabola di riferimento.
Distanze longitudinali nelle quali, agendo solo sul carrello Y ortogonale all’asse ottico, dovrei trovare le varie caustiche dei centri di curvatura delle finestre praticate nella maschera, che vanno via via a delineare il profilo della famosa “tromba”.
Per la misura delle prime due o tre zone a partire dal centro, aprirei alternativamente solo il post-it di una delle due finestre alla volta (per evitare di vedere fenditure sovrapposte e disturbate da frange di diffrazione dovute alla stretta fenditura, che renderebbero impossibile una precisa valutazione).
L’apertura alternata delle due finestre mi aspetterei che debba permettermi di trovare il miglior fuoco della sua immagine, tutt’al più con uno spostamento longitudinale del carrello che denuncerebbe però l’eventuale imprecisione della mia parabola in quella zona.TUTTO ciò nella speranza che gli spostamenti sull’asse ottico necessari, non stravolgano la misura.
Tuttavia nessuno degli utilizzatori della Caustica in Cloudy Nights cita il problema. E si potrebbe benissimo riaprire quella discussione con una domanda ai vari Guru che vi hanno scritto, per avere lumi.Grazie Giulio, ottima descrizione della procedura che tornerà sicuramente utile, purtroppo sono ancora fermo al “carissimo amico” , finchè non riesco a trovare un metodo/setup che dia la certezza di essere nel punto di fuoco di una zona è inutile tentare di fare una qualunque misura…
Un articolo interessante che descrive un metodo giuducato migliore della caustica per identificare il centro di curvatura delle zone , è quello descritto quiì:
http://bobmay.astronomy.net/DAFTtest/dafttest.htm
Purtroppo (per me) E’ scritto in un ignorante inglese terrificante, che lascia molto alla immaginazione.
Ma l’idea in sè non senbra malvagia, e consiste nel rendere molto evidente il centro di curvatura delle zone utilizzando un foro stenopeico al posto della fenditura, e di provocare la produzione di due serie di picchi di diffrazione (come quelli che provoca il supporto a croce del secondario), serie che si sovrappongono nel centro di curvatura alla moda della messa a fuoco con la maschera di Hartmann.
Il foro stenopeico è difficile da fare (e da illuminare). Se ne trovavno tanti microscopici smontando l’eletrodo frontale (di nastro metallico autoadesivo) che porta i forellini da cui escono lanciate dalla carica elettrostatica le goccioline di inchistro delle cartucce per stampanti ink-jet, del tipo che ha l’uggello integrato nella cartuccia (tutte le vecchie stampanti HP).
Invece la mia chiacchierata precedente era solo allo scopo di vedere se non ti suggeriva nulla quel passaggio che io non ho capito, riferito dal Lecleire per trovare il puno iniziale della caustica, con una sottrazione al valore di X trovato della metà del valore X teorico calcolato.
Interessante ma mancante di due elementi i quali modificherebbero nella realtà la figura osservata:
1- gli anelli di diffrazione con buona pace di Mr. Airy
2- il contributo degli altri fuochi oltre quello riferito alla parte centrale della zona.Comunque è proprio grazie a questi due elementi che si giunge ( era ora ) alla soluzione, la chiave è stata fornita ( come al solito
) da una tua riflessione, oltre che dall’aiuto delle attente considerazioni di Mirco:Giulio dixit: Per la misura delle prime due o tre zone a partire dal centro, aprirei alternativamente solo il post-it di una delle due finestre alla volta (per evitare di vedere fenditure sovrapposte e disturbate da frange di diffrazione dovute alla stretta fenditura, che renderebbero impossibile una precisa valutazione).
detto e fatto ho realizzato la stretta fenditure con due lame separate da qualche micron, in alcuni punti le lame erano a contatto spezzando la continuità della fenditura con dei piccoli fori separati da spazi scuri.
Riprendendo il punto 1:
le linee di diffrazione erano a quel punto ben visibili insieme a dei semi-anelli che si formavano intorno ai fori. Le linee e gli anelli restavano ben visibili nel solito intervallo di un millimetro ( più o meno ) di spostamento longitudinale per diminuire di visibilità fino a scomparire allontanandosi o avvicinandosi allo specchio.Riprendendo il punto 2:
Ogni zona contiene un settore parabolico e dato che i centri di curvatura di una parabola variano con continuità, anche l’immagine osservata all’oculare in questo test dovrà necessariamente mostrare i “fuochi” che si susseguono con continuità:
Ho realizzato una maschera con solo 4 fori circolari da 25 mm e questi effetti , come prevedibile, sono ancora più evidenti.combinando questi due criteri, si capisce come deve essere valutato il fuoco
a-non esiste un punto di fuoco univoco ( unico centro di curvatura ), perchè in quel caso il settore sarebbe sferico.
b-esiste un intervallo longitudinale che comprende tutti i centri di curvatura nella zona.
c-questo intervallo è facilmente individuabile dalla comparsa degli effetti della diffrazione
d-la micrometrica fenditura, all’interno di questo intervallo, non sarà mai visibile come una unica linea sottilissima, ma bensì come una linea (sottilissima ) e centrale contornata da “margini” ancora sfocati ( gli altri fuochi del settore ) e le figure di diffrazione. Questa situazione determina il “primo fuoco” ovvero il raggio di curvatura più corto tra quelli in esame.tutto questo è splendidamente riassunto nell’immagine tratta dagli appunti di Giulio ( credo che sia il testo dei LeCleire )
il mio errore era di tipo “culturale”
, ho infatti sempre cercato di vedere l’immagine della fenditura bella a fuoco, come avrei fatto osservando un qualsiasi oggetto all’infinito da un telescopio con specchio parabolico. Avrei dovuto ragionare come se dovessi cercare un fuoco in telescopio con forte aberrazione sferica.
Questo errato ragionamento mi ha portato finora a giudicare sfocate le immagini simili a quella nella foto.Tutto questo spiega anche perchè possa essere utilizzata solo una fenditura molto stretta o un foro stenopeico, in quanto l’immagine di un oggetto ( capello o similari ) o di una fenditura più larga, renderebbe indistinguibili i vari fuochi dando la sensazione di una immagine sempre definita in un certo intervallo longitudinale.
Dopo aver verificato il tutto questa notte
, credo di essere finalmente pronto ad iniziare la prima sessione di misura. la cosa simpatica ( si fa per dire… ) è che tutto questo discorso serve solo per identificare l’inizio della caustica
dopodiché non si devono trovare” a occhio” i fuochi delle zone !
Infatti , per ogni successiva zona da misurare,il carrello verrà spostato sul valore X teorico calcolato tramite formula. quello che si misura è solo la distanza Y tra le due fenditure. Se questa misura è superiore al valore teorico di Y, la figura in quel punto è sovracorretta, se è inferiore è sottocorretta
Considerando che io non ho nemmeno una zona centrale da misurare ( ho un bel foro ! )…
comunque era importante ( almeno per me ) per capire di cosa si sta parlando !
Sono molto felice che tu sia riuscito a superare la “Rupes recta” così velocemente.
Questa vicenda non fa che sottolineare come certi argomenti tecnici e pratici insieme, debbano essere vissuti in prima persona per poterli poi compiutamente descrivere in divulgazione, senza dare per scontato alcunchè, ma anzi specificando “quel che sembra ma non è”.
Sarebbe il compito del buon divulgatore o buon insegnante. Molti invece non “scendono” a questo livello più che naturale, perchè non ne hanno conoscenza o perchè non hanno passione.
Primo test:
Come prima prova, ho utilizzato la maschera con soli quattro fori da 25 mm per lato.
La difficoltà ed il buon esito del test è tutta nel trovare con precisione il fuoco della prima zona, operazione che va ripetuta all’inizio di ogni sessione, ci vuole un po’ di pratica e pazienza, ma una volta capito il “meccanismo” ci si arriva con una discreta sicurezza.
Tutto il resto è abbastanza semplice, non è richiesta alcuna capacità interpretativa, una volta trovato manualmente il primo fuoco, si posiziona il carrello longitudinale per ogni zona su valori preimpostati. In pratica ci si posiziona dove la teoria ci dice che dovrebbe trovarsi il fuoco della zona successiva. ( ed in effetti ci si ritrova proprio li… )
A quel punto ci vuole solo molta concentrazione a misurare con precisione la distanza tra le fenditure, ma con un buon riferimento visivo nel campo oculare non è assolutamente difficile misurare il centesimo di mm.
Ripetendo le misure ci si rende conto di quanto, a differenza del Foucault, le differenze tra i valori ottenuti siano molto contenute, finora il massimo scarto che ho ottenuto in una serie ripetuta di misure è stato di 2 centesimi ( Lo spostamento di un centesimo di mm visto all’oculare è superiore all’ampiezza della fenditura , quindi è uno spostamento ben visibile e controllabile ) . Facendo poi la media ci si ritrova con letture approssimate al micron.
questo il report dei risultati:
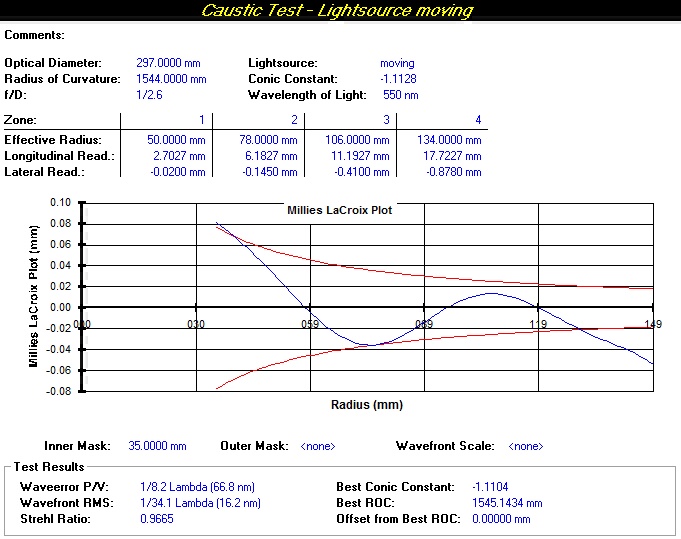
Chiaramente è una verifica molto approssimativa fatta su solo 4 zone, comunque in linea con i risultati del Foucault specialmente sul valore della costante conica, anche se l’iperbole ne esce un po’ “ridimensionata”
Domani si replica con maschera a 7 zone
Bellissimo!!
Ma cosa intendi quando dici “ma con un buon riferimento visivo nel campo oculare”?
In altre parole: Cosa intendi per buon riferimento visivo?Per quanto riguarda il ridimensionqmenro della curva, mi parrebbe che sia una logica conseguenza del fatto che con queste misure, e contrariamente al tuo precedente modo di procedere, tu sei partito dal centro.
….Sarebbe l’ideale che tu (pena un sicuro incasinamento nei calcoli delle X) continuassi ad andare a ritroso partendo dalla periferia….Ammesso che sia possibile come sembrerebbe a prima vista.si, a volte mi esprimo malissimo…
Intendevo il crocicchio/filo di rame o quant’altro si utilizzi come reticolo di puntamento per centrare la fenditura nell’oculare. Deve essere sottile, perfettamente a fuoco e allineato con la fenditura, pena una cattiva/incerta misura.
L’ideale sarebbe il tuo oculare del microscopio, con quello si potrebbero prendere le misure direttamente , in barba a eventuali micrometrici giochi meccanici.Ci avevo pensato di partire dal bordo , ma la messa a fuoco “manuale” e la relativa misura è più difficoltosa, il rischio di errori è più elevato.
Il ridimensionamento credo sia fisiologico,come dicevamo Foucault misura fino alla sovrapposizione delle fenditure e non tiene conto del “surplus” della caustica. Tutto sommato mi aspettavo peggio…
Sì vedo che non è male la tromba.
Pensavo che potesse essere possibile eseguire una normale “ANDATA” caustica da centro a bordo,ma una volta arrivato in cima, regolare la migliore visione della caustica di quella zona, e da quella nuova distanza calcolare con formule inverse le nuove X del percorso a ritroso.
Si l’oculare del microscopio mi pare sia un blocchetto estraibile d(e reinseribile) all’apparecchio senza problemi, come un cilindro diametro (vado a memoria) circa 15 mm e lunghezza circa 30mm
- Devi essere connesso per rispondere a questo topic.