TRADUZIONE IN ITALIANO DEL CAPITOLO 8 DEL LIBRO “LA CONSTRUCTION DU TELESCOPE D’AMATEUR”
di Jean Texereau
(NOTE: Pour les lecteurs de langue francaise, il est conseillè de lire cet article directement sur le livre nommè, (pages 137 – 149) pour eviter fautes dû a la double traduction automatique).
La difficoltà principale della costruzione di un telescopio in una combinazione Cassegrain o sua variante, è dovuta allo specchio secondario che è convesso, e di conseguenza non può essere controllato col Metodo di Foucault senza l’uso di costosi strumenti come componenti ottici ausiliari, poiché il test di Foucault è applicabile solo su specchi o superfici ottiche concave.
—————————
N.D.T: Farebbe però eccezione lo strano test applicabile in modo diretto secondo il metodo proposto nel 1945 da J. H. KING, descritto nella edizione 1998 del libro A.T.M. 1 a pagina p. 321, capitolo B.14 “Testing convex surfaces” secondo la seguente figura B.14.1, che consiste nell’installare lo specchio convesso (o la lente piano-convessa o bi-convessa da testare), in modo tale che essa chiuda con la faccia convessa rivolta all’aria ambiente, un tubo-serbatoio cilindrico di lunghezza determinata dal raggio di curvatura di quella faccia, che verrà riempito di liquido avente lo stesso indice di rifrazione del vetro in prova. All’estremo opposto il recipiente cilindrico verrà chiuso con una finestra ottica in vetro che sia perfettamente piana anche solo sulla sola superficie rivolta verso l’ambiente esterno al tubo. Finestra ottica che assicurerà la possibilità di eseguire attraverso di essa un normale test di Foucault della concavità interna allo specchio (o alla lente) visti da dietro, avendo il liquido di egual indice di rifrazione del vetro, resa invisibile, e di fatto fisicamente eliminata ogni riflessione proveniente da ogni superficie intermedia del percorso ottico immersa in esso, ad eccezione della estrema superficie convessa, che vista posteriormente si presenta concava.
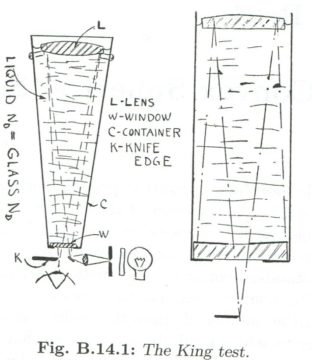

Le in genere piccole dimensioni di questi specchi non obbligano a contenitori stagni di grandi dimensioni, tuttavia la complicazione di questo test diretto sta nel trovare un liquido di riempimento di sicurezza ininfiammabile ed economico che possieda un indice di rifrazione identico (ma probabilmente anche solo il più possibile vicino) a quello del vetro in esame, sapendo che l’indice del vetro parte da quello del Crown (BK7) con valore 1,5, e sale al vetro normale calcio-sodico con 1,57, fino al denso Flint con valore 1,68. I più comuni liquidi trasparenti che si avvicinano abbastanza a quei valori, sono la trementina e gli oli minerali, come si legge sulle tabelline allegate alle istruzioni dei rifrattometri di uso industriale per le verifica della qualità degli oli minerali, come riportato dalla figura più sopra.
Fine della nota
—————————————————————-
Siccome la scelta del metodo di controllo influenza notevolmente l’intero svolgimento dei lavori, prenderemo in esame i quattro metodi pratici validi:
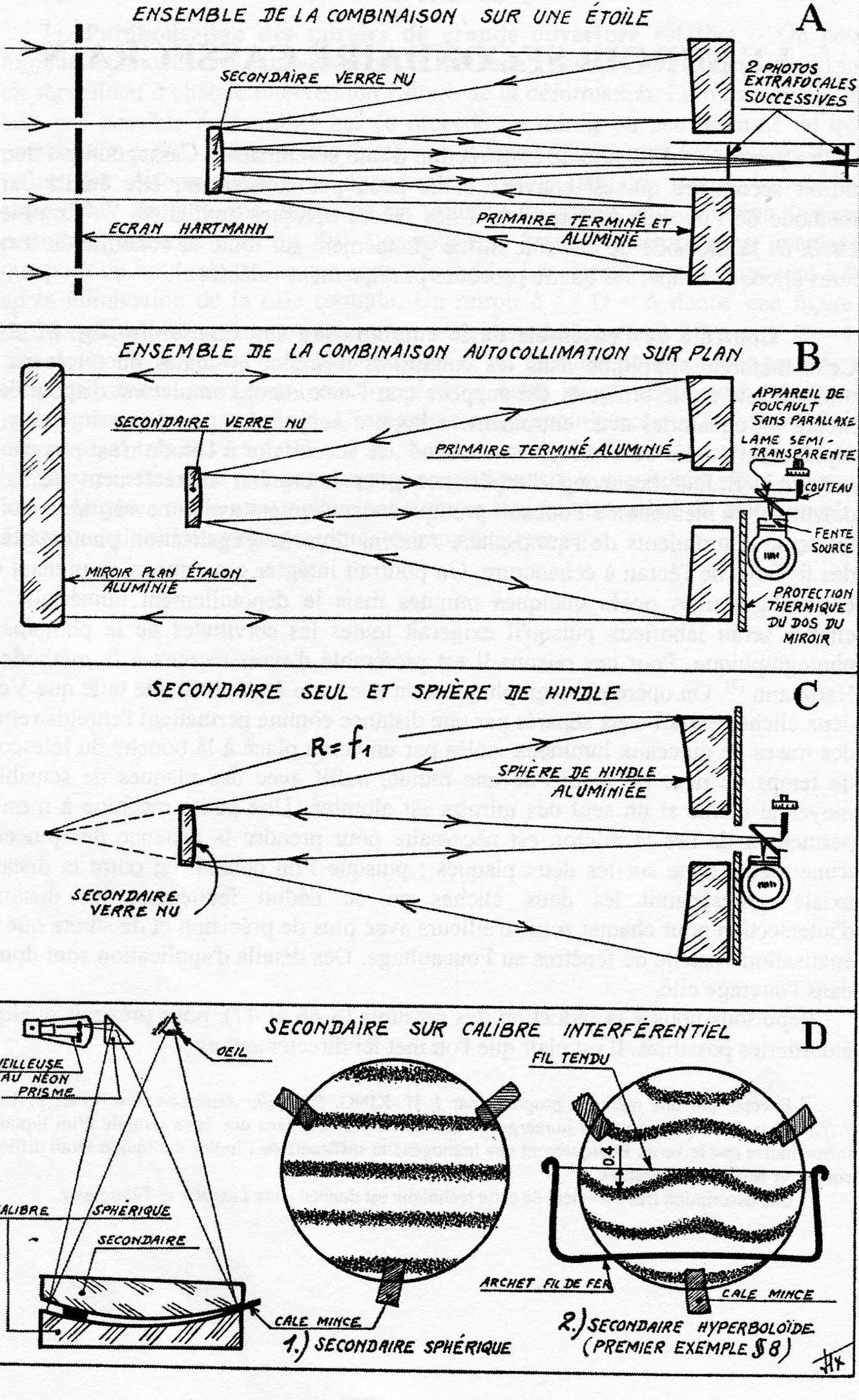
74. CONTROLLO “STAR TEST” DI TUTTO IL TELESCOPIO SU UNA STELLA (vedi seguente figura 82 A).
Questo metodo si applica nel normale uso del telescopio con una stella luminosa. Si presume che lo strumento completo sia disponibile e montato in montatura equatoriale ben stazionata e quindi mossa da preciso moto orario con lo specchio primario già realizzato e alluminato; mentre il secondario allo studio non è indispensabile che sia metallizzato.
Ci vuole moltissima esperienza per interpretare correttamente un piccolo difetto per mezzo dello star test, che è il metodo di Foucault praticato visualmente su una vera stella;
Questo perchè i vortici turbolenti e le correnti d’aria rendono illusoria la equalizzazione fotometrica che l’operatore deve compiere sulle ombre delle finestre dello schermo di Couder. Si potrebbero integrare questi vortici semplicemente riprendendo immagini (Foucault-grammi) formate da alcuni minuti di posa fotografica, ma il conteggio digitale sulle immagini sarebbe laborioso poiché esigerebbe la presa in considerazione di tutte le servitù di fotometria fotografica. Per questi motivi è preferibile usare il metodo di Hartmann (2), operando fotograficamente con una stella luminosa come Vega, che verrebbe ripresa in due immagini extrafocali separate da una distanza nota. In quel modo si sarebbe in grado di registrare tracce di “pennelli” o fasci luminosi isolati da uno schermo disposto alla imboccatura del telescopio, e sarebbe sufficiente un tempo di esposizione di circa un minuto con pellicola di media sensibilità, anche se solo uno degli specchi è alluminato.
Per misurare la distanza fra le immagini dei due fasci di una medesima zona occorre un micrometro in grado di leggete il micron; dal momento che inoltre si conosce la distanza assiale che separa le due immagini, si deducono facilmente le distanze di intersezione per ciascuna zona, anche con maggiore precisione e sicurezza di quella che deriverebbe dalla equalizzazione fatta in modo visuale, delle finestre al test di Foucault.
- Dettagli di applicazione sul metodo Hartmann sono dati nell’opera “Lunettes et telescopes” di Danjon e Couder.
Figura 82
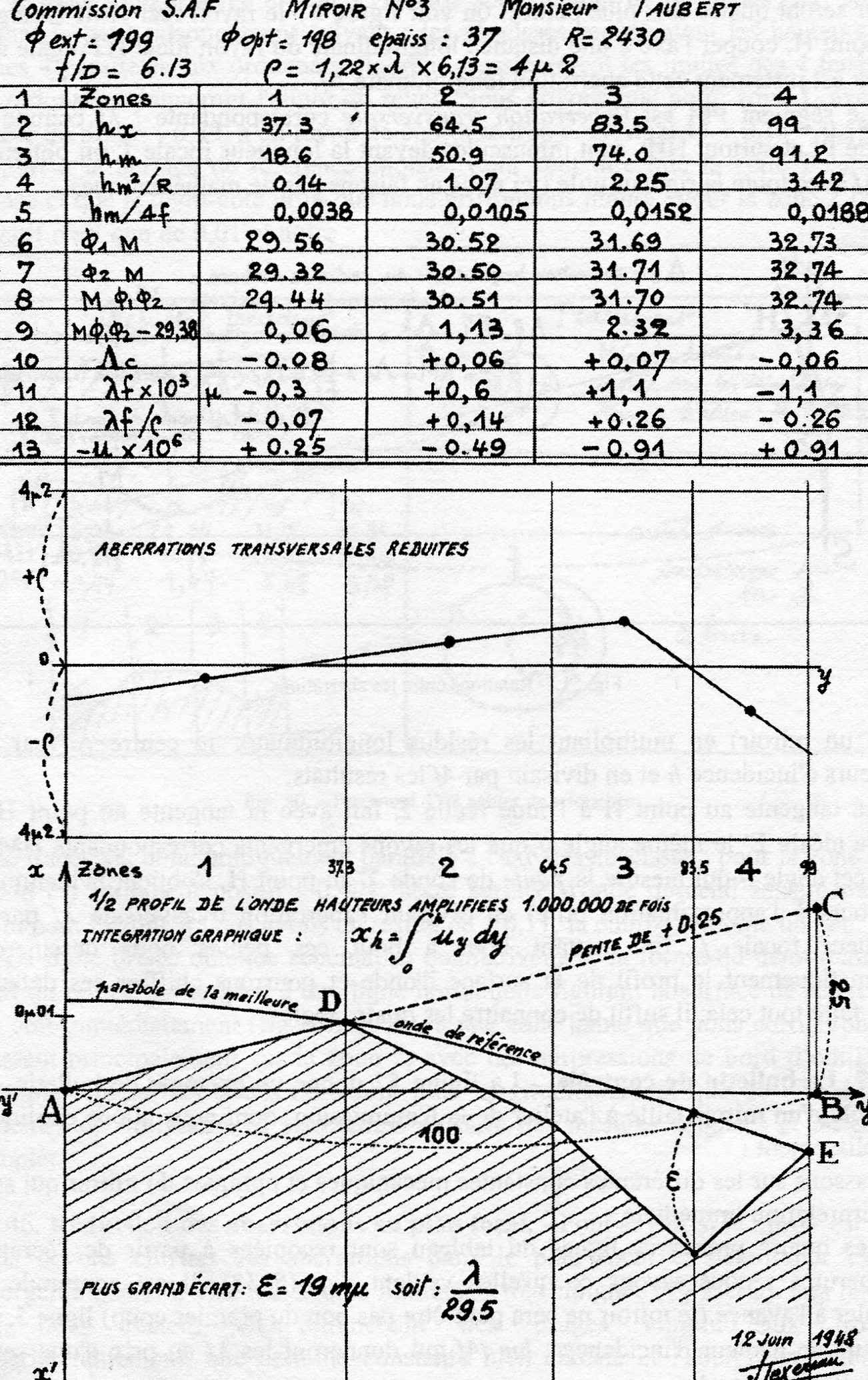
Per evitare possibili errori, è meglio rinfrescarci un attimo le idee riferendoci al contenuto del capitolo riguardante i calcoli per trasferire le aberrazioni al piano focale (riduzione delle aberrazioni al piano focale), ed al capitolo sulla redazione del bollettino di controllo, come visibile nella seguente figura 52 tratta da pag 85 del Texereau.
Figura 52 Bollettino di controllo
E ‘chiaro che in una prova con la sorgente posta all’infinito le aberrazioni sono al fuoco, e quindi non si ha da fare la sottrazione dei valori hm²/R in linea 4 di figura 52, che riguarda le sottrazioni che intervengono solo al centro di curvatura, cioè nel test di Foucault la cui sorgente non si trova all’infinito, ma anch’essa a quel centro, a fianco del coltello del tester.
Allo stesso modo per trovare rapidamente il piano del cerchio di minima aberrazione, poichè mettiamo in evidenza le aberrazioni longitudinali al fuoco (linea 5 fig 52), bisognerà utilizzare i valori di hm/F e non quelli di hm/4F.
Infine le aberrazioni longitudinali trasversali si troveranno utilizzando la seguente formula (16):
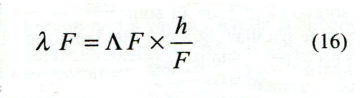
Gli altri calcoli del bollettino rimangono invariati.
Il vantaggio di uno studio diretto del telescopio nelle condizioni di impiego, è dato dalla presenza automatica delle aberrazioni termiche che intervengono realmente, e che in un grande strumento sono spesso importanti .
Purtroppo però con l’uso dello star test, il ciclo di controlli e di ritocchi rimane subordinato al bel tempo meteorologico.
(Il completamento di un secondario di un Cassegrain da 60 centimetri per l’osservatorio Meudon ci ha chiesto quasi sei mesi utilizzando solo questo metodo, mentre presso l’Osservatorio dell’Alta Provenza un mese fu sufficiente per un secondario di diametro di quasi 52 centimetri, per un telescopio Cassegrain di 193 centimetri).
Nel caso di un piccolo strumento è possibile evitare questa difficoltà se si ha a disposizione un locale chiuso ed abbastanza lungo da poter installare una stella artificiale ad almeno una trentina di metri di distanza.
Il Foucaultaggio visivo in quel caso riprenderebbe il suo vantaggio in quanto l’aria nella camera può essere mantenuta otticamente omogenea, cosa che non è generalmente facile ottenere all’aperto.
Una piccola maschera di Couder omotetica di una normale, può essere posizionata contro il secondario per la localizzazione diretta dei ritocchi da realizzare. La sorgente non essendo più all’infinito apparirebbe con una leggera sovra-correzione sferica, e l’aberrazione longitudinale sarebbe molto inferiore rispetto hm²/R, ma non necessariamente trascurabile.
75. Controllo dell’intera combinazione ottica (cioè del telescopio completo) per mezzo di uno specchio piano (vedi più sopra in figura 82 B) .-
Leon Foucault diceva che “uno specchio piano per l’ottica sperimentale è un cielo artificiale”. Se si possiede uno specchio piano senza difetti ed almeno di diametro pari a quello dello specchio primario Cassegrain, lo si può utilizzare per l’autocollimazione. Questo metodo è stato seguito da G. W. Ritchey in particolare per il controllo della combinazione Cassegrain del telescopio di 152 centimetri di Monte Wilson. Si utilizzerà un apparecchio di Foucault nel quale la sorgente e il coltello saranno più vicini possibile, o meglio totalmente privi di parallasse utilizzando un vetro semitrasparente (Fig. 82 B). Infatti se la sorgente è fuori asse le riflessioni simmetriche che avvengono colpiscono i nostri specchi in punti sostanzialmente differenti. Vediamo che ci sono in tutto cinque riflessioni, una prima volta il telescopio con la sorgente al fuoco, serve da collimatore per fornire dei raggi paralleli riflessi dal piano verso la combinazione che diventa telescopio.
I difetti sono quindi raddoppiati.
È necessario alluminare lo specchio piano e il primario per mantenere luce sufficiente. In mancanza di un insieme meccanico completamente realizzato, il montaggio deve comportare delle regolazioni fini per mezzo di viti agenti sui tre specchi, e malgrado ciò, quella collimazione costituisce un buon esercizio per un principiante.
Questo metodo, come quello sopra, non consente che il controllo del fascio assiale.
La frazione di secondario che eccede questo fascio (nel caso che si voglia estendere il campo) non può essere controllata in una sola volta.
Pochi dilettanti però possiedono un buono specchio piano di diametro pari al primario. Buono significa che i difetti zonali sono fastidiosi, ma una piccola curvatura del piano è irrilevante per l’auto-collimazione.
76. Metodo Hindle (vedi più sopra in figura 82 C) (2). – Si associa lo specchio secondario convesso da controllare, ad un grande specchio sferico speciale di prova il cui raggio di curvatura sia uguale alla lunghezza focale dello specchio primario del telescopio. La distanza d dei vertici è quindi la stessa nello strumento reale.
Questa volta sono presenti solo tre riflessioni, e il fascio passa due volte sul secondario raddoppiandone così i difetti.
Lo specchio sferico utilizzato in queste condizioni fornisce un equivalente fascio stigmatico della configurazione di un paraboloide con sorgente all’infinito. Il Foucaultaggio così rivela direttamente le carenze del secondario raddoppiate, come secondo nel metodo precedente.
Le misure devono essere fatte con una piccola maschera di Couder , con calcolo di riduzione delle aberrazioni come avverrebbe con un fascio incidente parallelo.
Con uno specchio sferico di Hindle un poco più grande dello specchio primario, si potrà controllare un secondario sovradimensionato per motivi di campo.
L’ovvio svantaggio pratico di questo metodo è la necessità di realizzare un secondo grande specchio per ogni configurazione di telescopio, perciò lo specchio sferico di Hindle è giustificato solo per una produzione in serie di telescopi Cassegrain standard.
(2) JH HINDLE “un nuovo test per il Cassegranian-gregoriano e specchi secondari” in Monthly Notices by Royal Astronomical Society, Marzo 1911, riprodotto in A.T.M.1. pag. 225.
77 Controllare un secondario su calibro concavo (Vedi più sopra in figura 82 D).
Questo metodo è stato trovato e insegnato da A. Couder nel 1945-1946 al laboratorio ottico dell’Osservatorio di Parigi. Ed è pure stato scoperto in modo indipendente da J. P. Hamilton che ne pubblicò una buona descrizione nel 1952 (1).
Le spiegazioni dei capitoli § 51 e 52 di pag 93 del libro del Texereau, al proposito di come si eseguono i controlli interferenziali su specchi piani con un interferometro di Newton facilmente auto-costruibile, ci permettono di essere brevi
(N.D.T. Vedi equivalenti articoli sui test interferometrici di Newton in questo blog https://www.grattavetro.it/interferometro-di-newton/ e https://www.grattavetro.it/frange-di-newton-concavita-e-convessita-delle-superfici-in-esame/ ).
Si incomincia col realizzare un piccolo specchio sferico concavo almeno grande quanto il convesso da costruire e con raggio r2 identico. La verifica della sfericità di questo specchio concavo con Foucault non presenta alcun problema, bisogna solamente stare attenti, con uno specchio così piccolo, alle aberrazioni extra-assiali del montaggio nel telescopio, che possono essere fastidiose se la sorgente non è vicinissima o confusa con l’immagine di ritorno.
Questo specchio sferico farà la funzione di calibro interferenziale.
Se lo specchio secondario convesso ha il dorso lucido e trasparente (vetro normale Saint-Gobain), le frange di interferenza possono essere osservate posizionando la sorgente di luce e l’occhio vicino al centro di curvatura del calibro. Tre distanziali di carta di cui uno più sottile separano le due vetri, e come al solito bisogna orientare verso di noi quello sottile.
Se supponiamo che il nostro specchio convesso sia sferico con lo stesso raggio del calibro, le frange di interferenza saranno rettilinee come per un vetro piano (vedi più sopra fig. 82 D1).
Ricordiamo che la frangia diametrale rappresenta la deformazione della sezione meridiana del vetro controllato.
Quindi ogni volta che questa deformazione in rapporto ad una linea retta raggiunge una inter-frangia, cioè la mezzeria fra due frange contigue, si deduce una differenza di Lambda / 2 che corrisponde a 0,3 μm con riferimento la lunghezza d’onda efficace della luce al neon data dalla lampada usata nell’interferometro.
(1) J. P. HAMILTON. “Un test per il secondario Cassegrain”. in Il giornale della astronomic Society of Victoria. Febbraio 1952, p. 7.
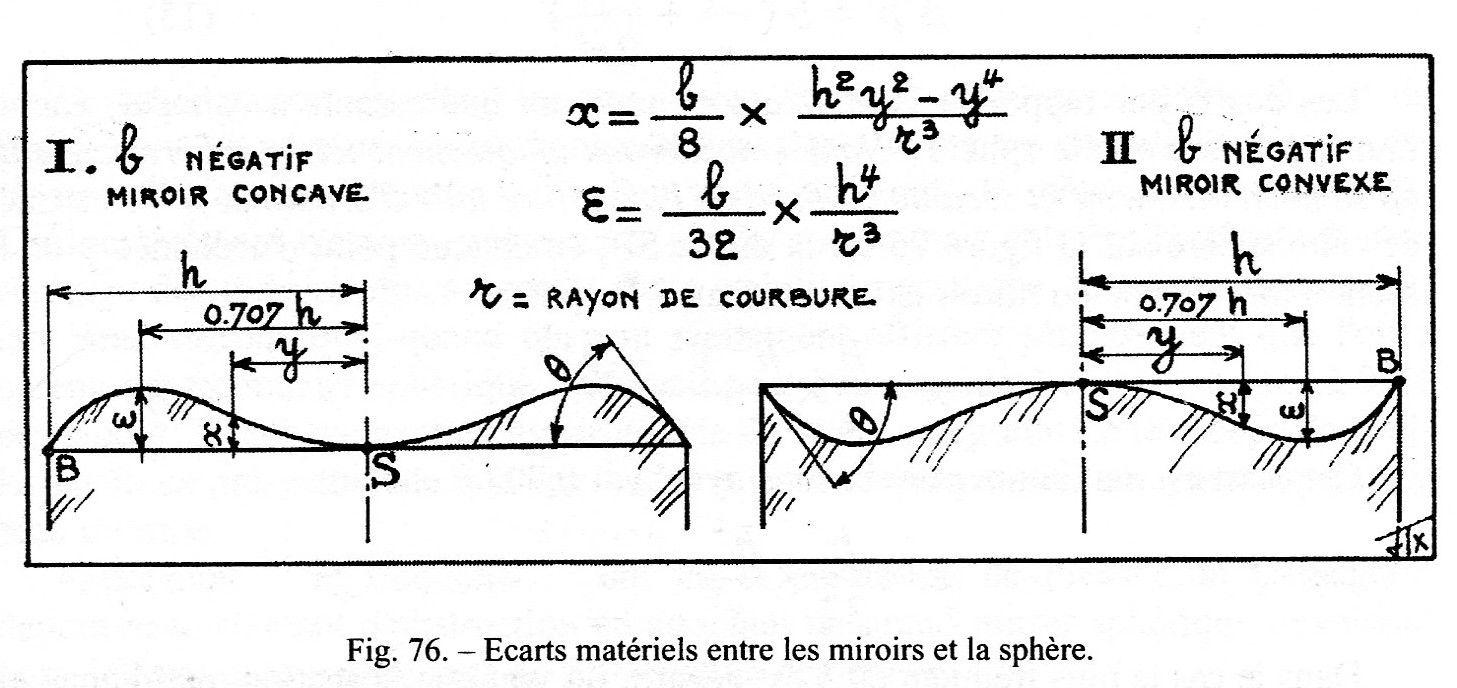
Specialmente se vogliamo verificare che il secondario sia iperbolico, basta vedere se la frangia centrale disegna bene l’andamento della seguente figura 76 II quando il distanziale di carta sottile (in figura chiamato “cale mince”) è posizionato come mostrato più sopra nella figura 82 D2;
Inoltre, il divario massimo per la zona 0.7 può essere stimato in decimi di inter-frangia e confrontato con la deformazione calcolata con la seguente formula (15), dove b è il noto coefficiente di deformazione della curva.

Per esempio, le frange rappresentate più sopra in figura 82 D2 si riferiscono allo specchio secondario della combinazione proposta come primo esempio costruttivo a pagina 128 del libro del Texereau, per il quale ε vale 0,12 micron, ossia (0,12μ x0,3) = 0,4 inter-frange.
Si nota che il presente metodo richiede la realizzazione di uno specchio convesso con un raggio di curvatura rigorosamente imposto ed identico a quello del calibro concavo realizzato.
Per soddisfare a questa concordanza corrispondente alle frange della precedente FIG. 82 D, si è spesso portati dei ritocchi più laboriosi della iperbolizzazione propriamente detta.
Infatti è possibile controllare l’iperboloide anche se alla deformazione si aggiunge la differenza di curvatura di alcune frange tra lo specchio e il suo calibro. E’ quindi sufficiente calcolare il contorno delle nuove frange di uguale spessore (nota 1).
(1) Questa famiglia di curve è dato fino a ± 2 frange nell’articolo di J. P. HAMILTON citato sopra.
Se si preferisce operare con distanziali di uguale spessore occorrerà calcolare il cambiamento di diametro dei nuovi anelli di Newton corrispondenti alla deformazione.
Per questi motivi noi preferiamo regolare il raggio di superfici a meglio di una frangia di vicinanza, prima di iperbolizzare. Questo permette un controllo più diretto e più sicuro della deformazione, Comunque, l’approssimazione al decimo di inter-frangia è cosa sufficiente per un modesto telescopio.
Nel caso di una notevole deformazione può essere preferito figurare il calibro concavo che è facile da controllare in modo esatto con Foucault, utilizzando una maschera di Couder come per un paraboloide, ma utilizzando i valori di Δ p’ calcolati dalla seguente formula (13) di p.127, e il valore di B2 del secondario.

Il secondario sarà da ritenersi completato quando osserveremo delle frange dritte sul calibro deformato.
Questo metodo è più facile da implementare per un dilettante privo di vetri di controllo.
Diamo ora gli aspetti pratici del lavoro nel caso che si scelga questo metodo di verifica.
78 Metodo generale di lavoro di piccoli specchi convessi.
I secondari di telescopi amatoriali diametro 200 oppure 300mm hanno generalmente un diametro compreso fra 30 e 80 mm. Realizzare esattamente uno di questi specchi è più difficile di come si potrebbe supporre non avendo esperienza in questo lavoro.
Il processo di lavorazione a posto fisso su tavolo, se risulta semplice ed efficace quando si lavora un disco di 200 x 35mm diventa sempre più difficile e incerto se si scende sotto 150 e soprattutto sotto i 100 mm di diametro.
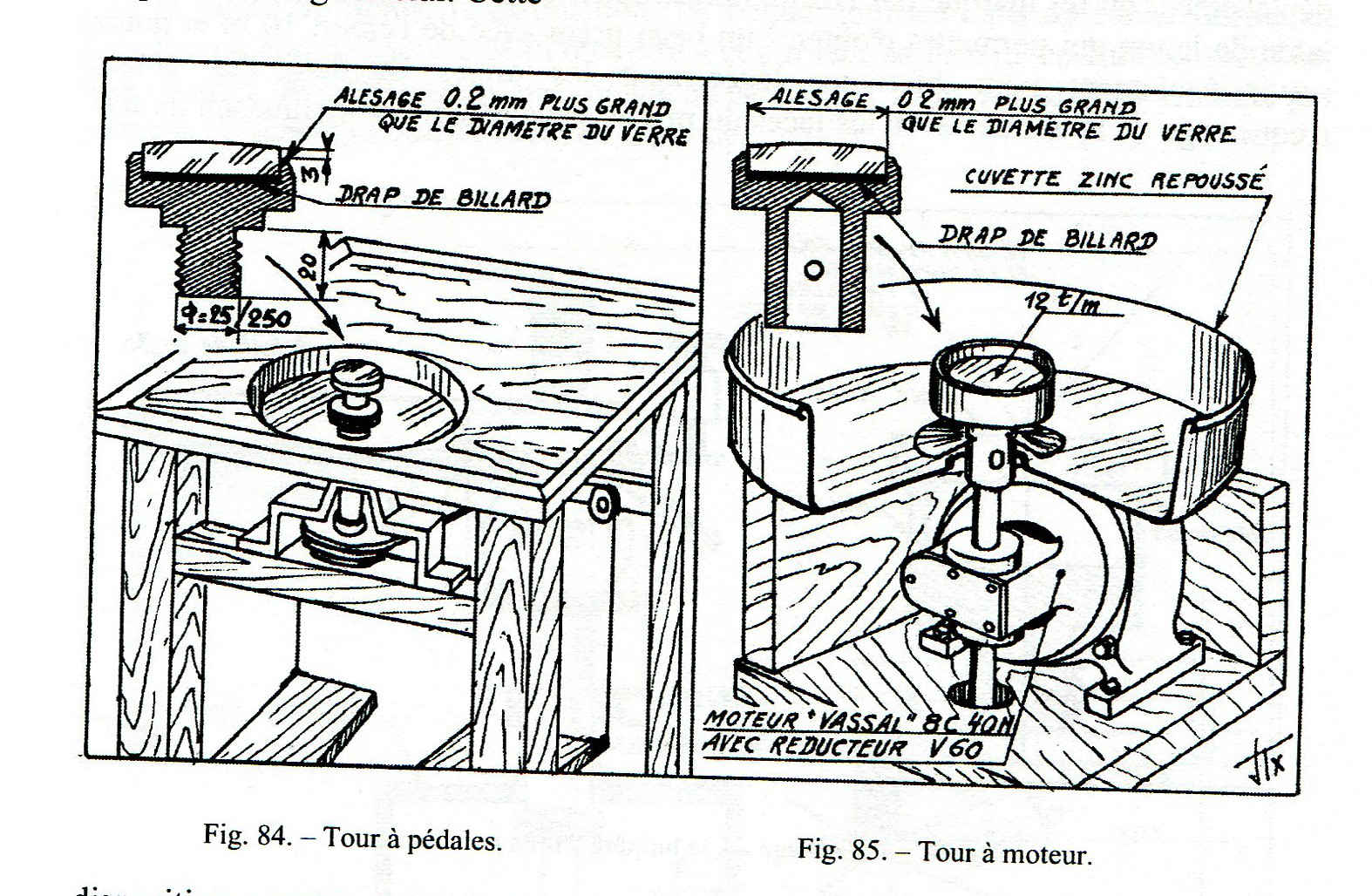
Infatti con specchi così piccoli e leggeri, le pressioni involontarie delle mani portano a spostamenti dei pezzi in lavorazione e a sorprese sgradevoli. Invece il lavoro da seduto di fronte al vetro dove l’utensile ruota lentamente su un asse verticale, rende le cose molto più facili. Il tornio a pedale per ottici della seguente figura 84, è infatti considerato la migliore macchina per piccoli lavori di ottica di precisione (2).
Disponendo si un tale tornio si sceglierà la velocità più lenta e l’azionamento dei pedali più lento e costante possibile almeno durante la lucidatura di precisione.
È tuttavia possibile improvvisare un tornio per un lavoro casuale, utilizzando direttamente l’asse lento di un moto-riduttore a vite senza fine, a condizione che la sua rotazione non superi 15 giri / min (vedi seguente figura 85).
Figure 84 – 85
(2) Produttori clave, 9, rue Olivier Metra, Paris 20 °
Uno di tali torni e lucidatrici industriali include un porta pezzo con un codolo del diametro standard solitamente filettato come possiedono molti utensili per tornio. I vetri da lavorare sono fissati ad esso per mezzo di colle a base di pece o di colofonia come quella denominata “cemento per ottici”, o quella che i francesi chiamano “Arcanson”(1).
Noi preferiamo montare i vetri da lavorare senza vincoli mediante speciali adattatori a scodella che ricevono le lenti su un disco di stoffa senza stringere.
Questo fissaggio (indicato in figura 85) consente di controllare o invertire i vetri in lavorazione senza doverli scollare e ri-incollare ad ogni inversione di posizione. Esistono scodelle di adattamento in lega leggera o semplicemente in legno duro, che possono essere montate direttamente sull’asse rotante del tornio, o semplicemente essere attaccate sopra un piano rotante presentato da un eventuale utensile esistente della macchina (vedi figura 86).
79 Lavorazione di affinazione del bordo grezzo.
Per realizzare specchio e utensile può essere utilizzato come materia prima uno scarto di lavorazione in vetro normale Saint-Gobain da 10 a 15 mm di spessore.
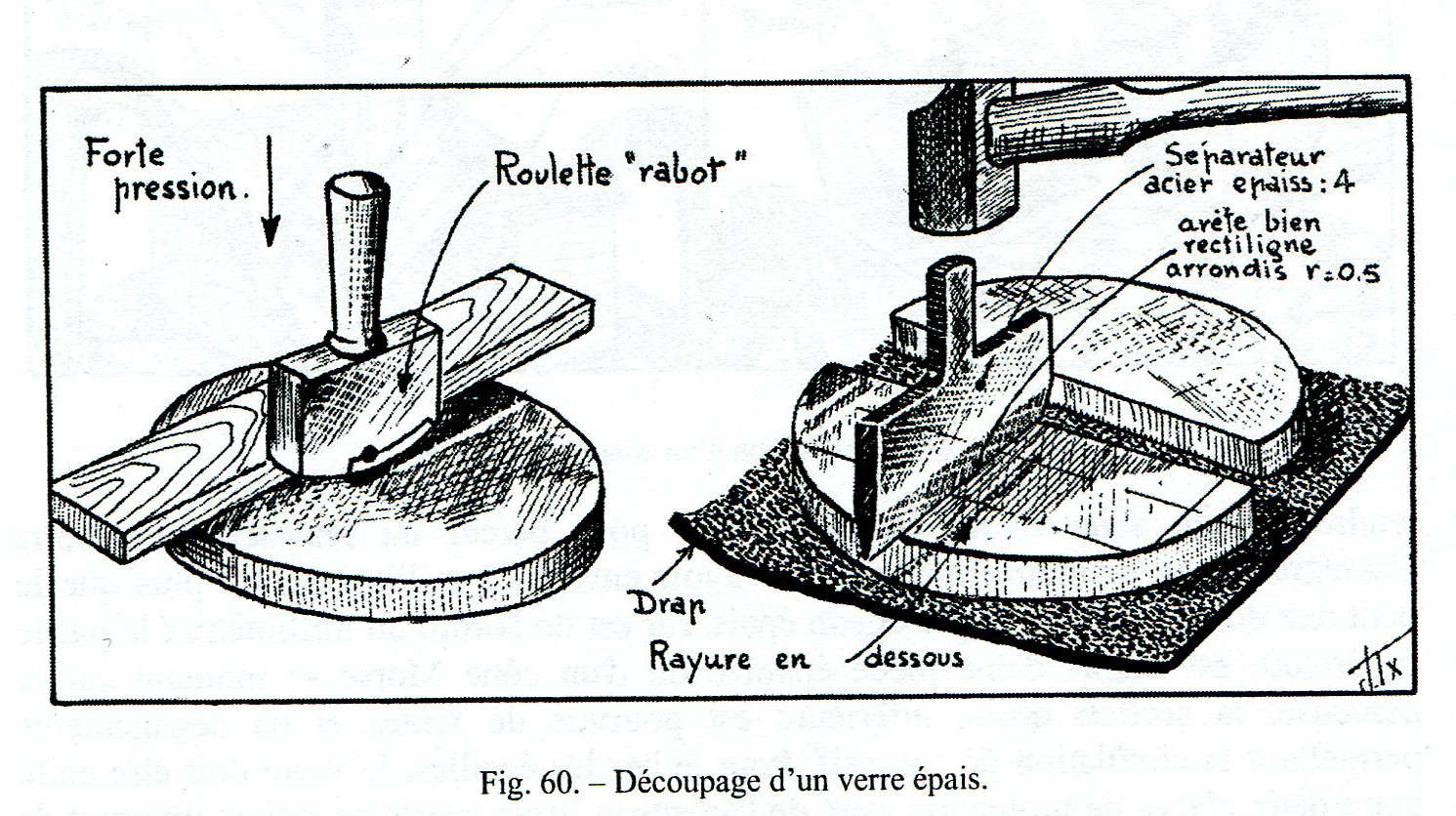
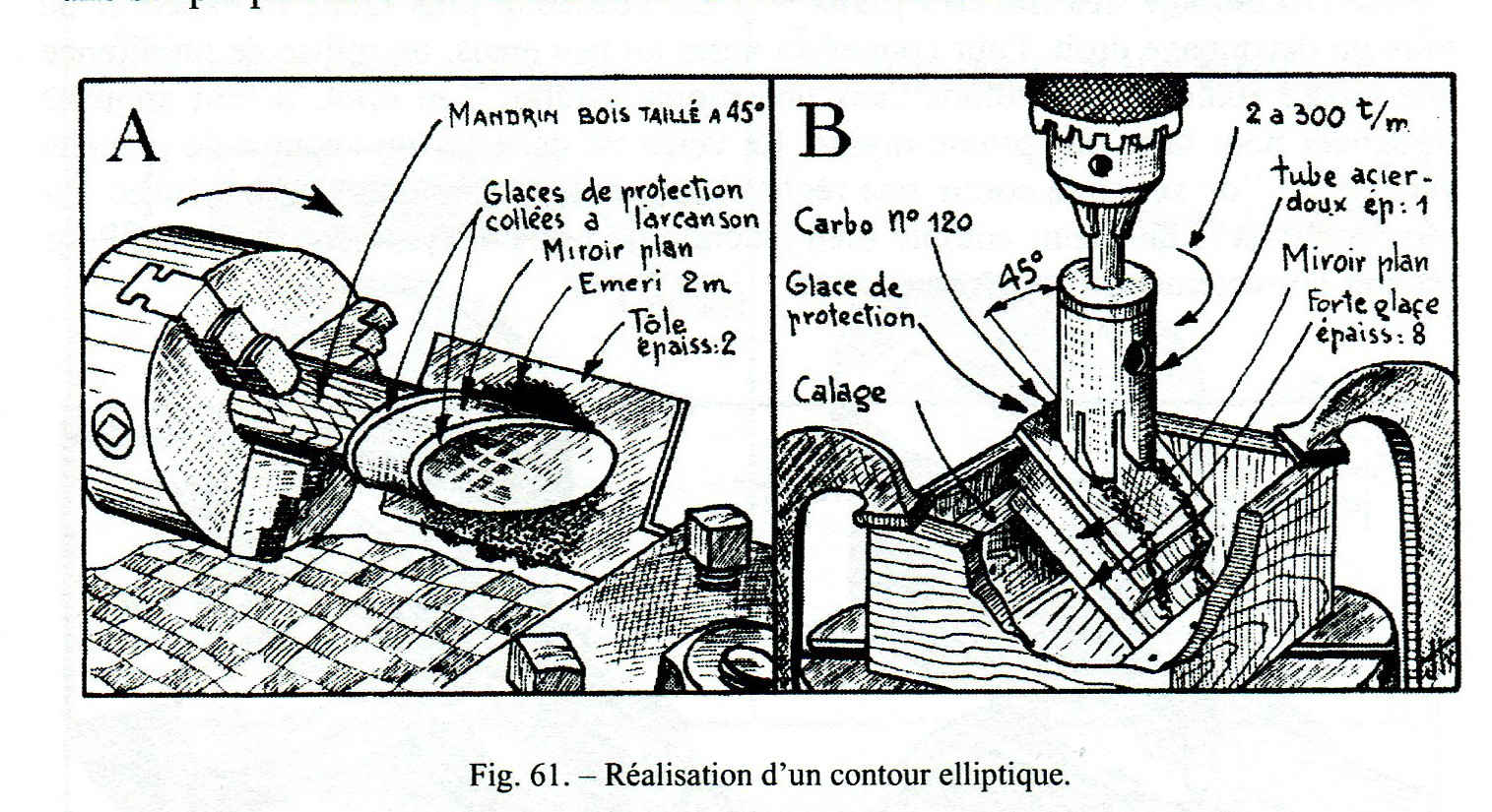
Dopo il taglio sommario col classico tagliavetro a ruotina o a diamante (fig 60), oppure con la carotatrice fatta con un semplice tubo di ferro a tazza che taglia a umido per interposizione di grana smeriglio (Fig. 61) il vetro ricavato è incollato alla colofonia sulla ruota porta pezzo del tornio (fig. 86). Prima che la colofonia si raffreddi completamente, si deve correggere la posizione del vetro in modo che le facce che verranno lucidate girino ben centrate sul supporto, per assicurare sia una rotazione centrata che ortogonale all’asse della macchina.
Un modo classico per verificare che questa centratura e ortogonalità sia soddisfatta, consiste nell’assicurarsi della immobilità della immagine della riflessione di una lampada o di una finestra, data dalla faccia superiore del vetro in rotazione.
Questa centratura detta “alla luce” viene fatta con grande cura per una lente che deve essere centrata fin dalla sua costruzione, destinata ad esempio all’inserimento in un sistema ottico che preveda una forte convergenza, ma qui nel nostro caso dello specchio secondario, un controllo di massima è ampiamente sufficiente.
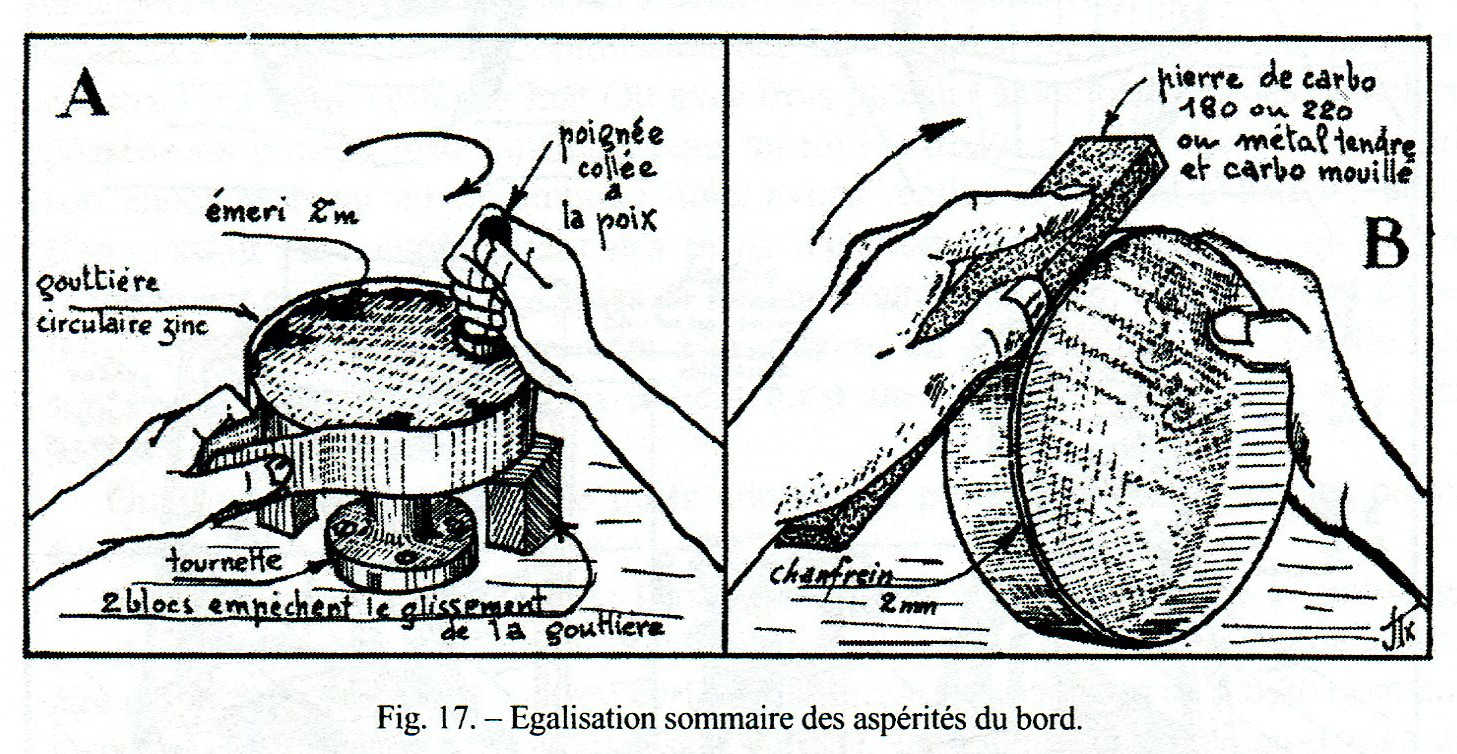
Bisogna attendere il completo raffreddamento del colofonia prima di intraprendere il rodaggio / affinamento / regolarizzazione del bordo del vetro. Se quest’ultimo è irregolare si inizia con una equalizzazione sommaria con una fascia di zinco (vedi seguente Fig. 17 A), utilizzando uno smeriglio di grana 1 minuto, azionando il tornio ad una velocità di circa 100 giri / min.
(1) Per i dettagli su queste opere classiche, consultare la Guida al lavoratore del vetro ottico di precisione, scritte dal colonnello DEVE (Ed. optical Review).
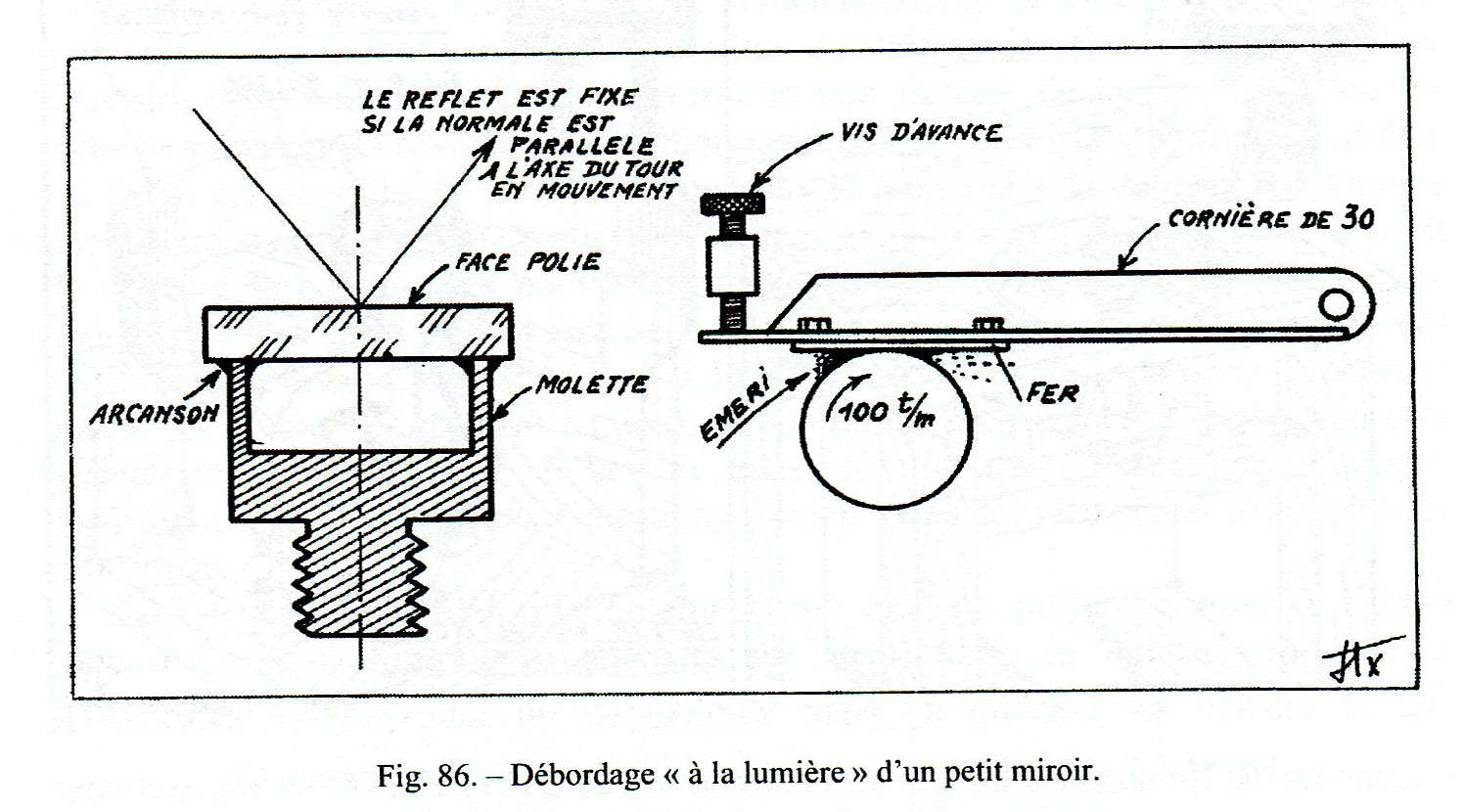
Ma per rendere il vetro esattamente cilindrico conviene un approccio tangenziale con un ferro articolato su un punto fisso, e spinto da una vite di avanzamento (vedi seguente figura 86). Si utilizza lo smeriglio di grana 1 minuto oppure 2 minuti fintanto che il rumore dell’abrasione rimane discontinuo, ad indicare che è ancora discontinua la superficie da uniformare al semplice contatto del ferro rivestito con smeriglio e bagnato, senza pressione.
Il cambiamento di grana dello smeriglio sarà accompagnato da uno spostamento del ferro mobile corroso dall’usura tangenziale, oppure questo sarà sostituito con una lama in ottone che fornirà una bella grana con smeriglio 10m e potrà pure servire per smussare leggermente i bordi che sono sempre fragili.
I difetti di squadratura del bordo dello specchio vengono corretti inclinando il ferro.
80 sgrossatura.
La lavorazione vetro su vetro fornisce contemporaneamente due pezzi interessanti che sono ambedue lucidati applicando il controllo col metodo della interferenza di cui al (capitolo § 77)
(N.D.T. Vedi equivalenti articoli sui test interferometrici di Newton in questo blog:
https://www.grattavetro.it/interferometro-di-newton/ e https://www.grattavetro.it/frange-di-newton-concavita-e-convessita-delle-superfici-in-esame/ ). .
Il vetro convesso sarà lo specchio, la cui parte posteriore piana, che dovrà essere lucidata, sarà protetta da una vernice di gommalacca contro posibili danneggiamenti derivanti dalla lavorazione della faccia anteriore. L’utensile concavo verrà successivamente lucidato a diventare calibro, ed è vantaggioso che esso venga realizzato circa il 10% più grande dello specchio, cosa che non disturba l’abrasione e permetterà di trascurare un eventuale errore di inopportuno bordo ribattuto.
La sgrossatura avviene come al posto fisso, il vetro che dovremo rendere convesso è posto di sotto, vale a dire supportato dal porta pezzo del tornio.
Data la piccola quantità di vetro per rimuovere, lo smeriglio 1m oppure 2m e le corse importanti 4/5D ma poco decentrate , sono sufficienti ad ottenere rapidamente la curvatura desiderata.
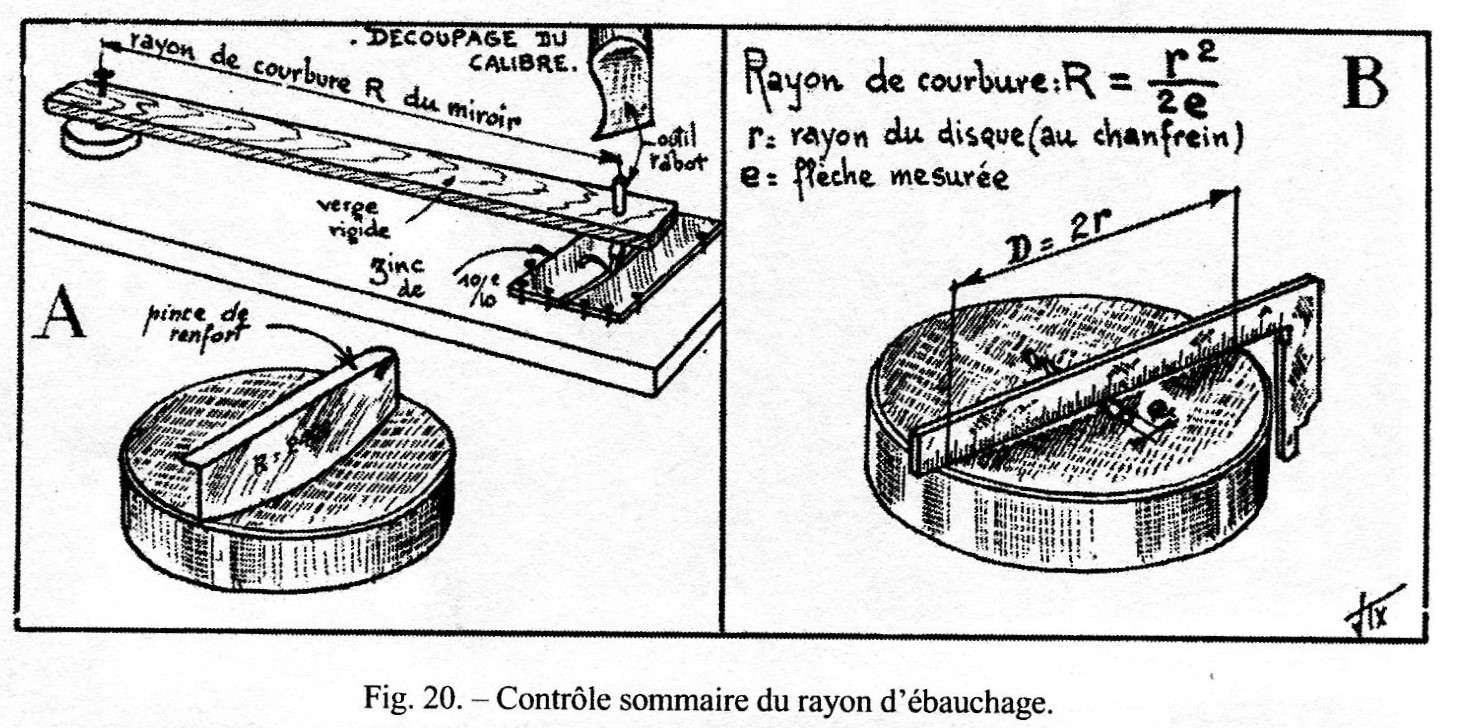
Per la verifica del raggio di curvatura raggiunto in questa fase, e sufficiente utilizzare una maschera o un modello di cartone o di zinco tagliato direttamente al raggio di curvatura r2 calcolato.
Raggiunta la curvatura desiderata occorrerà regolarizzarla applicando le solite corse con ampiezza 1/3 D . Con le stesse corse si regolarizza la superficie nella inversione della posizione dei vetri che necessitano di due adattamenti differenti sulle due facce.
Dopo la solita meticolosa pulizia e le relative precauzioni che evitano rigature indesiderate, si può passare agli smerigli grana 5 e 10m mettendo però in opera delle corse un poco più corte delle 1/3D a causa del fatto che l’utensile concavo che è più grande del nostro specchio, ha la tendenza negativa ad abbattergli il bordo.
L’inversione della posizione specchio – utensile deve essere utilizzata non solo per correggere un raggio di curvatura troppo lungo o troppo corto, ma anche sistematicamente ad ogni seccata per mantenere esattamente identici i raggi di curvatura complementare dei due vetri.
La precisione del controllo possibile con un semplice modello della curva in cartone o lamierino di zinco (Fig. 20 A, pag. 33) lascia a desiderare per la verifica precisa del raggio di curvatura d’un secondario Cassegrain. La lunghezza focale risultante e i punti coniugati sono sensibilissimi a questo parametro.
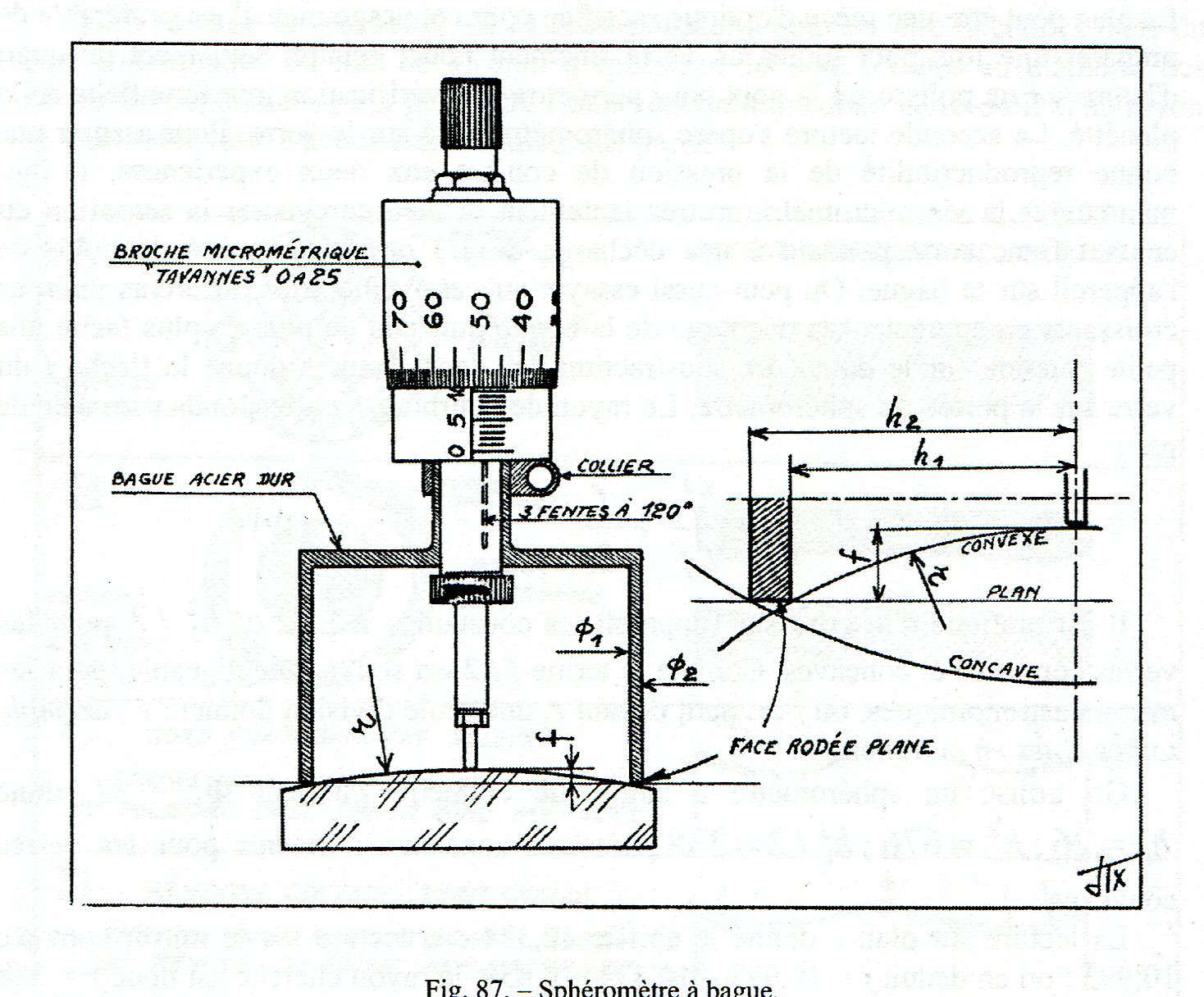
Perciò, per misurare con la dovuta precisione la freccia, può essere utilizzato uno sferometro a tazza come si vede in figura 87.
La tazza tornita in acciaio duro, ha un diametro un poco inferiore a quello del vetro da testare; la sua superficie di contatto anulare viene rettificata dopo cementazione e/o tempra e finita di lappatura con smerigliatura di grana 5 e 10 m, per esempio su un piano in ghisa, e il bordo che definisce la circonferenza della superficie di contatto della tazza deve essere ben vivo.
81 Sferometro a tazza (o ad anello) vedi precedente figura 87.
Come si vede a destra in fig.87, una testina di misura micrometrica permette di misurare questa costante con una precisione nel caso di vetri convessi, di Ø1/2 = h1 e di vetri concavi di Ø2 / 2 = h2.
La tazza è provvista di fessure assiali a 120° per assicurare elasticità e centraggio ad un fissaggio con fascetta tipo collare metallico che la unisce ad una testina di misure micrometrica tipo Palmer.
Questo dispositivo di misura si adatta molto facilmente ad una varietà di strutture, ad esempio per i controlli di spessori o di parallelismo di lastre di quarzo per filtri birifrangenti, o per lastre di chiusura di telescopi, oppure per lame di Schmidt, lenti di obiettivo, ecc …, non esitiamo a consigliare la migliore vite possibile. Ad esempio un passo di 1 mm, è preferibile a quello di 0,5mm, il tamburo cromato deve essere di grande diametro per consentire una facile interpolazione delle letture al micron fra tacca e tacca.
Nel caso che vi sia preoccupazione di incorrere in un errore di costante nella misurazione un vetro concavo di piccolo raggio, la punta del tastatore della testina di misura micrometrica (cioè la punta di contatto dell’asta di misura), deve essere ridotta al diametro massimo di 2mm, oppure anche lucidata come una piccola area della superficie convessa. Mentre invece sarebbe inutile la complicazione costruttiva di un tastatore non rotante con la vite di misura. L’esecuzione della misura dovrebbe permettere una rotazione estremamente morbida della vite.
Malgrado qualunque cosa ne possano dire i trattati di misura meccanica, se si evita di utilizzare il limitatore di coppia dell’apparecchio (che di solito è sempre regolato troppo duro) è possibile definire un contatto con una fedeltà di un micron con la semplice padronanza della durezza di manovra del tamburo delicatamente manipolato.
Una prima lettura serve per annotare la misura corrispondente all’azzeramento del contatto della vite con il bordo della tazza, e si fa con lo sferometro posato su un piano di riferimento. Il piano può essere un pezzo ottica sacrificato a questo scopo, ma è meglio preparare una volta per tutte un vetro smerigliato finemente in superficie e lucidato solamente per un quarto d’ora con un utensile di pece, per consentire la verifica interferenziale della planarità.
La seconda lettura è fatta trasferendo lo sferometro sul vetro da misurare.
(N.D.T: Con l’azzeramento dello sferometro il bordo della sua tazza viene a trovarsi allo stesso livello della punta del tastatore centrale; mentre invece quando lo strumento è posto sul vetro convesso esso toccherà inizialmente solo sul tastatore che verrà arretrato dalla rotazione del micrometro fino a che il bordo della tazza non raggiunga il contatto con il vetro).
Per assicurare buona riproducibilità della pressione di contatto dei due esperimenti di misura, è necessario manovrare la vite micrometrica molto lentamente e registrare la sensazione di franco contatto avvenuto, corrispondente a uno scarico di 1/3 oppure la metà del peso dello strumento sul bordo della tazza.
Si possono anche provare successivamente i differenti microns crescenti apprezzando lo scarico del peso dello strumento che rende via via sempre più facile una rotazione della vite di manovra sulla superficie lucida.
La sottrazione delle due letture ci fornisce la freccia f nel campo di applicazione dello sferometro.
Il corrispondente raggio di curvatura r è calcolato con la seguente (19):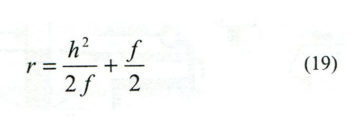
E’pratico registrarsi sull’apparecchio le costanti h12/2 e h22/2 per i vetri convessi e concavi. Siccome il termine f / 2 è spesso trascurabile per gli specchi astronomici nei quali F è piccolo rispetto a r, una sola divisione fornirà r come nel seguente esempio ove tutte le misure sono in mm:
Viene utilizzato uno sferometro a tazza di diametro interno dell’anello Ø1 = 52mm, così h1= 26; h12 =676; h12/2/ =338 è la costante da ritenere per i vetri convessi.
La lettura sul piano ha dato la cifra 10,334;
la lettura sullo specchio convesso 10,993.
Se ne deduce f = 10,993-10,334 = 0,659
il raggio cercato è quindi = 338 / 0,659 = 513.
Se vogliamo evitare ogni nociva approssimazione di calcolo, spingeremo la divisione a un decimale in più, qui scriveremo 512,9 e aggiungeremo f / 2, vale a dire 0,3 che dà un raggio più accurato di 513,2. Ma non dobbiamo mai dimenticare il significato fisico della misura limitata alla sensibilità di un micron, che rappresenta qui una approssimazione di ± 0,8 mm sul raggio (1).
82 affinamento.
Fin dall’inizio dell’affinamento della superficie è necessario rispettare il raggio di curvatura finale con la migliore approssimazione possibile. Ciò permette di invertire spesso la posizione utensile e specchio, e conduce più facilmente ad ottenere superfici perfettamente unite, cioè identiche ma complementari, vale a dire aventi esattamente lo stesso raggio di curvatura.
- lo sferometro a flessione di A. Couder permette di ravvicinare solo al decimo di micron, mentre gli strumenti comparatori a quadrante non sono generalmente fedeli al meglio di diversi micron, tranne quando le staffe di supporto sono molto rigide.
Per specchi così piccoli, 2 o 3 seccate di ciascuno smeriglio 20m e poi 40m sono sufficienti a uniformare le superfici. Il controllo finale del raggio di curvatura deve concentrarsi sullo specchio e sull’utensile. Dobbiamo fare in modo che le frecce si trovino esattamente concordanti (naturalmente tenendo conto della diversa costante dello sferometro). Infatti, con la finissima grana abrasiva di lucidatura sarebbe già difficilissima da realizzare una correzione di soli 2 μ, cioè di circa 7 frange. Un incontro di uniformità perfetto tra i due dischi può essere ottenuto con uno smeriglio più fine: 60 m o “304” conducendo parzialmente l’ultima seccata di lucidatura per metà con l’utensile sopra e per metà invertendo con lo specchio sopra.
83 lucidatura e ritocco.
I due utensili possono essere ricavati ad esempio da due dischi in legno compensato di spessore 15 mm torniti su una faccia esattamente al raggio di curvatura (verificato con buona esattezza con la maschera-modello in cartone o zinco) e torniti pure al diametro dei vetri corrispondenti per permettere la inversione immediata della posizione vetro – utensile
I due dischi in legno devono essere impermeabilizzati (un tempo si faceva per immersione completa in paraffina, oggi ci sono le vernici poliuretaniche).
Si comincia con una ricopertura della curva degli utensili con una colata di pece senza quadrettature.
Per fare la colata occorre disporre una fascia di contenimento di nastro adesivo di carta alto 50mm sul perimetro dei dischi in legno creando un recipiente in cui versare la pece fusa fino allo spessore di circa 6mm.
Appena il raffreddamento è sufficiente si può togliere il nastro adesivo di contenimento.
Si procede quindi ad un pressaggio della pece sulla curva del vetro inizialmente con una forte pressione con interposto un foglio di carta-seta / foglio di polietilene da cucina.
Infine si toglie la carta o polietilene e si esegue una pressione di migliore adattamento con la pece precedentemente pennellata di abrasivo cremoso (di solito ossido di cerio e acqua).
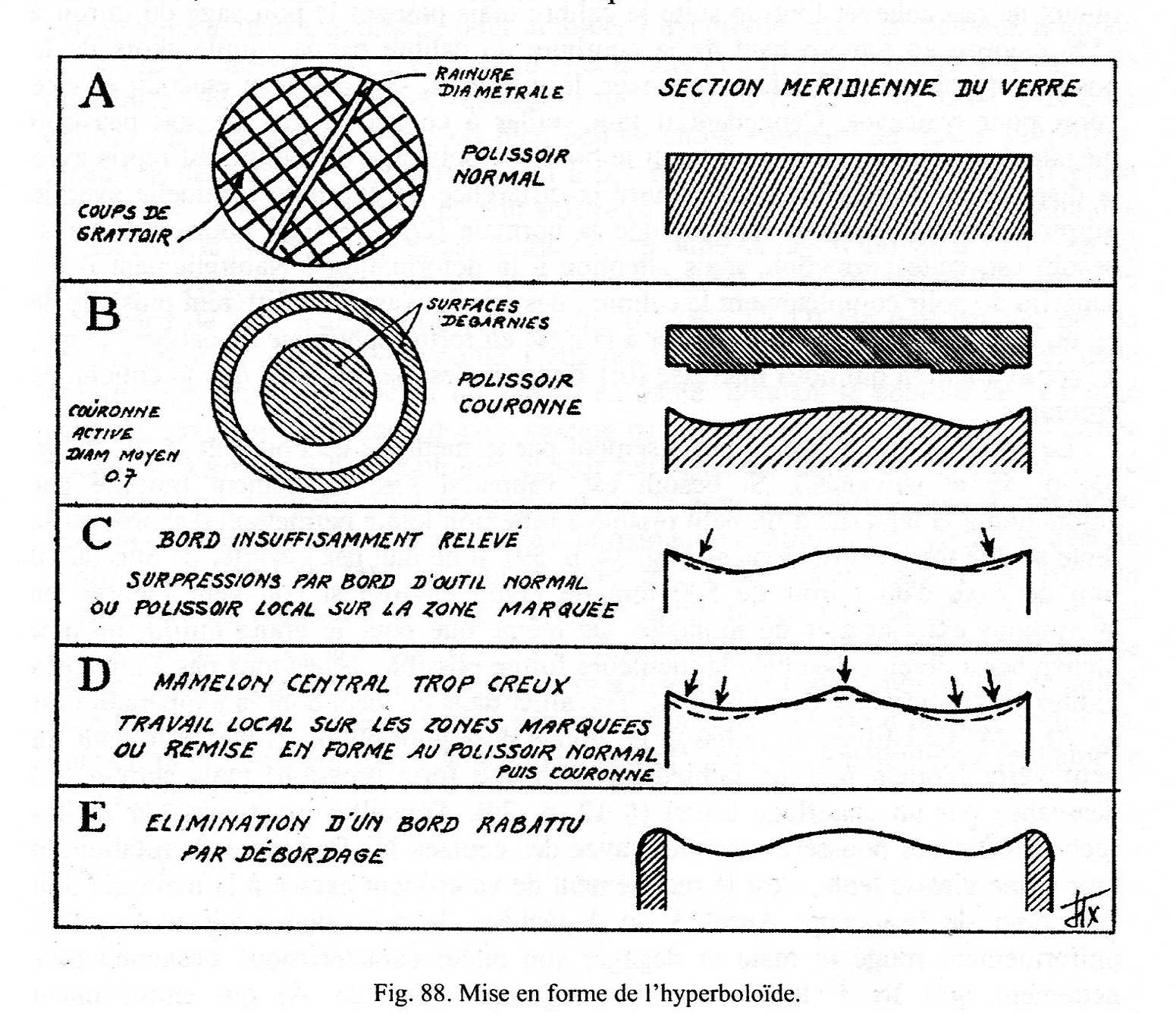
Si può quindi praticare una scanalatura diametrale, oppure una quadrettatura scavando dei solchi, (figura 88 A) o una spirale un poco incavata realizzate con un raschietto molto tagliente. Queste depressioni sulla pece devono essere mantenute o rifatte regolarmente durante tutta la lavorazione per migliorare l’aderenza.
(N.D.T. Le scanalature o depressioni devono imperativamente sempre essere presenti nella lavorazione degli specchi ottici, e servono ad evitare errori zonali dovuti alla possibile irregolare usura della pece, che potrebbe gonfiare in alcuni punti o viceversa perdere il contatto in altri).
Siccome la preoccupazione principale è di sapere se i vetri hanno dei raggi di curvatura sufficientemente vicini, si comincia con il lucidare sommariamente ma uniformemente su tutta la superficie, prima il calibro utensile e poi lo specchio per ¼ d’ora ciascuno, per poi procedere a un primo sommario controllo interferenziale.
Se esso indica una differenza significativa nella curvatura maggiore di 8 o 10 frange, è meglio riprendere la lucidatura per ottenere una unificazione dei vetri con maggiore esattezza.
Una differenza di curvatura concava – con i vetri che si toccano al bordo – è più difficile da recuperare che una convessità relativa; E’ anche auspicabile iniziare con una convessità 3 o 4 frange, che porterà a una lucidatura più facile.
Essendo le correzioni di curvatura tanto più agevoli quanto più i vetri non sono completamente lucidi, è meglio non lavorare subito il calibro, ma spingere la lucidatura dello specchio a circa il 75%, avvicinandosi poi alla curvatura del calibro per mezzo della semplice scelta della posizione sotto oppure sopra di specchio-utensile.
Se occorre aumentare la convessità, lo specchio convesso ben inteso deve stare sotto; e viceversa per aumentare la concavità del concavo. Tuttavia, dobbiamo lavorare in modo che il grigio (inteso come superficie ancora opaca) non sia troppo inegualmente distribuito tra il centro e il bordo.
La lucidatura del calibro avviene con la disposizione (sopra o sotto) conveniente per ridurre le differenze di curvatura residua rispetto allo specchio; Potranno essere utili a questo scopo delle corse più lunghe del normale (da 2/3 a 3/4 D) che aiuteranno se necessario la correzione, ma occorre prestare attenzione alla deformazione! Naturalmente è superfluo lucidare completamente il calibro; non appena i vetri non differiranno che di uno o due anelli bisognerà procedere alla messa in forma sferica del calibro, che ha l’approssimazione che ci interessa (0,1 frange). Ma questa non è una operazione così facile come può credere chi non ha esperienza.
Il controllo del calibro è fatto agevolmente con il metodo di Foucault (con le modalità descritte nel capitolo § 29 e fig. 33, di pag. 55 e seguenti).
Figura 33
Se necessario, il tester sarà leggermente modificato ruotando verso il coltello l’uscita della sorgente luminosa e installando un piccolo prisma a 90° di riflessione totale che permetterà di avvicinare fino a pochi millimetri il raggio luminoso della fenditura all’asse ottico e al coltello (Si tratta cioè di ridurre al meno possibile la quota asse lampada – coltello indicata in 25 o 30mm nel seguente disegno costruttivo del tester di Foucault in figura 34).
Se si vogliono contenere a quantità ignorabili le aberrazioni extra-assiali del montaggio, bisogna ridurre la distanza fra sorgente, coltello e asse l’asse ottico, a meno di 10mm per uno specchio di circa 500mm di raggio,
Figura 34
Analogamente allo specchio primario, si deve cercare di ottenere subito la migliore forma possibile. E’ bene non esitare a compiere qualche ripetizione data l’importanza di questo risultato. Lavorando preferibilmente in una stanza dove la temperatura sia da 20 a 24 ° C.
Utilizzare un utensile con buona pece pura, piuttosto un poco dura per un vetro piccolo (l’unghia del pollice deve segnare leggermente la pece sotto una forte pressione), ma soprattutto utilizzare pece non essiccata da un troppo repentino riscaldamento perchè avrebbe perso l’elasticità garantita dai solventi volatili perduti.
Lavorare con corse 1/3 D per piccole seccate spinte però lungamente nel tempo. Utilizzare una bassa velocità di rotazione del tornio, E’ il movimento avanti e indietro praticato mano che deve essere vincente.
Dopo 3 o 4 seccate la pece deve avere una superficie uniformemente incrostata di abrasivo (ad esempio ossido di Cerio), ed emanare il suo caratteristico odore di conifera molto di più di quanto lo emetta a freddo.
Occorre vigilare di rinnovare i canali ostruiti della pece (vedi precedente figura 88 A) in modo che l’utensile mantenga buona aderenza.
Il lavoro è impostato dalla quantità di abrasivo (ossido rosso di Ferro oppure bianco di Zirconio o Cerio) con acqua, così come è determinante anche la percentuale dei due componenti che metteremo in ogni seccata. Occorre infatti una seria esperienza per intrattenere delle seccate efficaci ed un utensile impeccabile.
I principianti mettono spesso troppo abrasivo alla volta o troppa acqua; Nel corso del lavoro, per completare una seccata deve risultare sufficiente una sola pennellata di abrasivo sul vetro.
Credendo di applicare questi consigli alla lettera, molti sono sorpresi da difetti zonali che appaiono irriducibili e che si generano regolarmente, la cui colpa può essere un regime termico insufficiente (dato da pece troppo dura o lavoro troppo breve o seccate insufficienti) che si traduce spesso in una superficie con bordo ribattuto e centro in rilievo (vedi precedente figura 33 D).
Il ritocco del centro in rilievo non è difficile, e si fa con specchio sotto e utensile sopra e corse centrate. Per quanto riguarda il bordo ribattuto, del quale sconsigliamo il ritocco su un piccolo vetro, si potrà anche trascurare se l’eccedenza del diametro del calibro sarà sufficiente, se no si deve riprovare migliorando la propria tecnica.
Una volta che il test di Foucault mostri che il calibro è ben sferico nella porzione utile (vedi precedente figura 33 C ), non resta che completare la figurazione dello specchio convesso. Le frange di interferenza osservate tra il calibro sferico e lo specchio attuale rivelano in generale un insieme di differenza di curvatura e una deformazione a volte usata direttamente per avviare la iperbole. Ma il metodo normale più sicuro è quello di correggere subito la curvatura per portare lo specchio sferico ad ottenere le frange rettilinee della precedente figura 82 D.
Non resta quindi che realizzare l’iperboloide, che è ben poca cosa a paragone del lavoro precedente.
Quando la deformazione non supera 0,l a 0,2 frange può risultare sufficiente un ritocco effettuato col pollice o coll’indice (§ 43). Ma in generale è meglio sguarnire l’utensile normale in forma di corona di raggio medio 0,7 (fig 88B); impiegato poi con corse un poco corte da ¼ a 1/3D.
Oltre alla verifica della differenza di quota massima ε sulla zona 0,7 (precedente figura 82D), si deve verificare che la curvatura presenti l’andatura desiderata.
Coloro che non sono molto familiari con questa deformazione possono tagliare in una maschera di carta la curvatura della frangia centrale per una data inter-frangia calcolata con la seguente equazione:

la figura 88 fornisce qualche esempio di iperboloide e del loro ritocco.
In figura 88 C il bordo in rilievo è insufficiente, un utensile locale agente sulle zone da deprimere potrà completare l’azione dell’utensile a corona. Qualche volta è il rilievo centrale che non viene col profilo esatto (fig 88 D), si può tentare un ritocco locale, ma è spesso consigliabile riprendere la messa in forma dopo un ritorno verso la sfera.
Certi operatori, qualsiasi cosa facciano, non riescono a evitare il bordo ribattuto. Quando questo difetto non è interamente nascosto dalla montatura, resta loro la possibilità di realizzare lo specchio secondario con un diametro sovradimensionato (vedi fig 88 E) per poi utilizzarlo solo sul diametro utile mascherando o asportando la zona tratteggiata in fig.88 E.
***