In questo articolo vorrei approfondire un aspetto riguardante l’interpretazione delle frange di interferenza, per mezzo dell’interferometro di Newton, durante l’analisi delle superfici ottiche.
Come già descritto in questo articolo, la valutazione del profilo della superficie convessa la si esegue andandola a confrontare con una superficie di riferimento (concava) che può essere sferica, parabolica o della stessa costante conica della superficie da analizzare a seconda del grado di deformazione dell’otica.
Una volta terminata la lucidatura del calibro concavo e ottenuta la forma desiderata, con precisione di almeno lambda/10, si piò passare ad analizzare la superficie dello specchio tramite le frange di interferenza che restituiscono una sorta di linee di livello corrispondenti alla distanza esistente tra le due superfici sotto analisi.
Questo tipo di test viene spesso utilizzato anche per testare la planarità di una superficie ottica. In questo caso però, sarà necessario disporre di un calibro con una superficie di riferimento piana (con precisione di almeno lamda/10) su cui si adagerà la superficie da analizzare per ottenere le frange di interferenza e quindi le informazione per determinare la forma dell’ottica sotto analisi.
Le forme classiche che le frange possono assumere in questo caso sono riportate nella tabella sottostante, suddivise in due colonne: una senza presenza di tilt (No inclinazione) tra le due superfici e l’altra con presenza di tilt (inclinazione tra le due superfici).
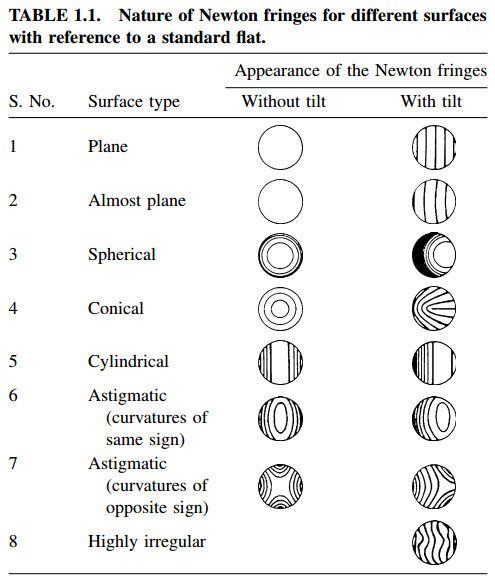
Nella figura sottostante invece, possiamo vedere un esempio di frange di interferenza tra due superfici, una otticamente piana e quella sotto esame.

Come è possibile osservare le linee non sono perfettamente rettilinee e questo indica la non perfetta planarità della superficie in esame, che nel caso specifico risulta avere una deviazione massima rispetto alla superficie piana di una quantità pari circa a lambda/4 (questo perchè la massima distorsione della linea centrale è pari a circa metà della distanza tra una frangia e l’altra, e tra una frangia e l’altra c’è sempre una differenza di 1/2 lambda).
Ovvero la superficie sotto esame non è piana, ma è da considerarsi come una superficie sferica avente un raggio di curvatura grandissimo, tanto da essere quasi piana.
Il raggio di curvatura di questa superficie però, potrebbe essere sia di una superficie concava che di una convessa (rispetto al piano) e presenterebbe le stessa forma delle frange di interferenza in ambedue i casi.
E’ necessario quindi disporre di un metodo che consenta di discriminare tra le due possibilità.
Il metodo consiste nel esercitare una leggera pressione sopra alle superfici durane il test, ed osservare in che direzione si muovono le frange.
Questo metodo lo si può eseguire sia esercitando la pressione in prossimità del bordo sia esercitando la pressione in corrispondenza del centro dei vetri ottenendo i seguenti risultati.
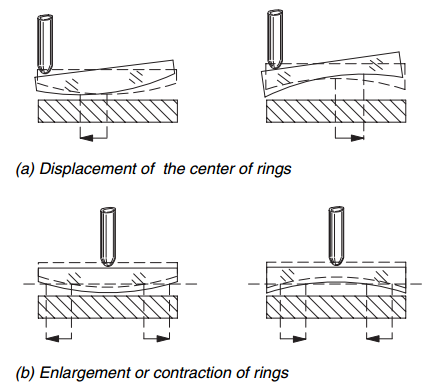
Come è possibile vedere dalla tabella soprastante se si preme in prossimità del bordo e le frange si muovono in direzione opposta al punto di applicazione della pressione significa che la superficie sotto analisi è concava, mentre se si muovono verso il punto di applicazione della pressione la superficie è convessa.
Se invece la pressione è esercitata al centro, si vedranno le frange circolari muoversi verso il centro se la superficie è concava e verso l’esterno se la superficie è convessa.
N.B: fare molta attenzione al significato di concava e convessa in questo particolare procedimento di analisi, in quanto può portare a errori grossolani di interpretazione, soprattutto quando sotto analisi non ci sono due superfici piane ma due superfici sferiche (paraboliche, iperboliche ecc…)
Per togliere ogni dubbio da errate interpretazioni ricordare sempre che:
- Superficie sotto analisi convessa = i due specchi si toccano al centro e c’è gap ai bordi.
- Superficie sotto analisi concava = i due specchi si toccano ai bordi e c’è gap al centro.
Tramite queste considerazioni è poi possibile capire se la superficie sotto analisi abbia raggio di curvatura maggiore o minore rispetto a quella del calibro e viceversa.
Esistono anche altri semplici test che permettono di discernere un’ottica concava da una convessa di cui se ne può trovare una descrizione tra le pagine da 6 e 10 del seguente libro: “Optical shop testing” di Daniel Malacara, dal quale state tratte tutte le immagini presenti nell’articolo.