Dimensionamento della Cella dello specchio primario con GUI PLOP

CHE COS’E’ GUI PLOP:

GUI PLOP è un potente programma per il progetto e la valutazione qualitativa della cella di supporto dello specchio primario del telescopio.

Perchè può essere critica la meccanica della cella di sostegno dello specchio?

Chi è del mestiere è a conoscenza del fatto che la precisione ottica di un obiettivo riflettore per  telescopio di qualità “appena accettabile”, consiste nel presentare un difetto SUL VETRO della sua superficie riflettente (inteso come misurazione “picco-valle” della sua peggiore asperità supeficiale), tale da non eccedere i 68,75 nanometri, ovvero milionesimi di millimetro, che degradano l’ ONDA RIFLESSA di un valore pari a un quarto della lunghezza d’onda (lambda) di 550 nanometri  posseduta dalla luce riflessa di colore giallo-verde, a cui l’occhio umano è più sensibile: Cioè il famoso “lambda/4.

E ciò è dovuto al fatto che l’onda, nel venire riflessa, viene danneggiata due volte dall’errore sul vetro: Una prima volta in incidenza ed una seconda emergendo da essa.   

E questo doppio danneggiamento dell’onda incidente ed emergente dimostra che per mantenere sull’onda un difetto di riflessione di Lambda/4 , è necessario che il vetro possieda una accuratezza doppia, e cioè Lambda/8, dato che:

Lambda/8 + Lambda/8 = Lambda/4.

Ovviamente, trattandosi di raggiungere almeno la precisione dei 68.75 milionesimi di millimetro di tolleranza, le prestazioni dello specchio possono essere sensibilmente influenzate anche da deformazioni non proprie dell’ottica, ma indotte da un mediocre sostegno dello specchio, che nella sua cella può essere portato a flettere quando varia il suo assetto puntando oggetti che stanno allo zenit o altri che stanno all’orizzonte.

Queste possibili flessioni generano un ulteriore errore che si somma a quello proprio della sua superficie, degradando potenzialmente le prestazioni dello strumento.

Chi è l’autore di GUI PLOP?

Il programma è il frutto del lavoro di diverse persone. Come di legge nella finestra “About Plop”, quelle citate per prime per importanza sono l’autore del programma David Lewis e l’ingegner Toshimi Taki.

Quest’ultimo è progettista aeronautico giapponese con l’hobby dell’astronomia, ed ha modificato a questo scopo uno specifico strumento di lavoro dei progettisti moderni, che è il metodo di calcolo strutturale degli “Elementi Finiti” , per poterlo applicare per  progettare e verificare le celle di supporto degli specchi per telescopi, in modo tale da minimizzare le distorsioni introdotte dalle loro sollecitazioni che influenzano negativamente le prestazioni ottiche.

Una di tali celle di supporto infatti, è caratterizzata dal sostenere lo specchio primario in una serie di punti del piano, la cui disposizione è calcolata al fine di caricare su ciascuno di essi, una quota parte del peso dello specchio anche al variare del suo assetto, tale da generare la minima distorsione della supreficie riflettente  (in funzione del numero di punti di appoggio scelti), e con tale distorsione visualizzare l’errore di riflessione ottica espresso in RMS, oppure in valori di rapporto picco/valle, che andranno a sovrapporsi agli altri errori della superficie, contribuendo al degrado delle prestazioni dello strumento.

Cos’è il “Calcolo strutturale degli Elementi Finiti”?:

E’ lo studio del comportamento sotto carico di un elemento strutturale complesso sollecitato dai suoi supporti (nel nostro caso, lo specchio) , che viene quindi suddiviso in una RETE di migliaia di componenti di dimensioni discrete, il cui comportamento sotto carico è descrivibile con l’approssimazione di equazioni algebriche, solo con la potenza degli attuali calcolatori. Equazioni che lo descrivono, giungendo a visualizzare in diversi colori il diverso grado di deformazione delle diverse zone sollecitate della superficie in esame.

All’astrofilo a cosa serve GUI PLOP?

Il programma permette valutazioni tecniche approfondite che vanno molto oltre le conoscenze BASE del normale astrofilo auto-costruttore. Tuttavia, in ambito “fai da te” astronomico amatoriale, GUI PLOP è molto utile per dimensionare il progetto della la cella del primario del proprio telescopio.

Ma l’uso del programma non è così “amichevole” ed immediato. Per cui persone non più giovani come me, che lo utilizzano molto raramente, nel tempo, dimenticano il “come si fa”.

Questo è il motivo che mi spinge spesso a scrivere delle istruzioni “pro memoria” a beneficio di me stesso. Cui ricorrere nel tempo in caso di futura necessità.

Il presente scritto è quindi uno..

 PSEUDO TUTORIAL PER L’USO DEL PROGRAMMA GUI PLOP

…Limitato ad un esempio pratico di dimensionamento della cella di uno specchio primario Newton Ø300mm con 9 punti di sostegno (ma vedremo che all’utilizzatore è tuttavia riservata la possibilità di scegliere il numero dei punti di appoggio desiderabili per confrontarne i loro valori e scegliere quello ottimale).

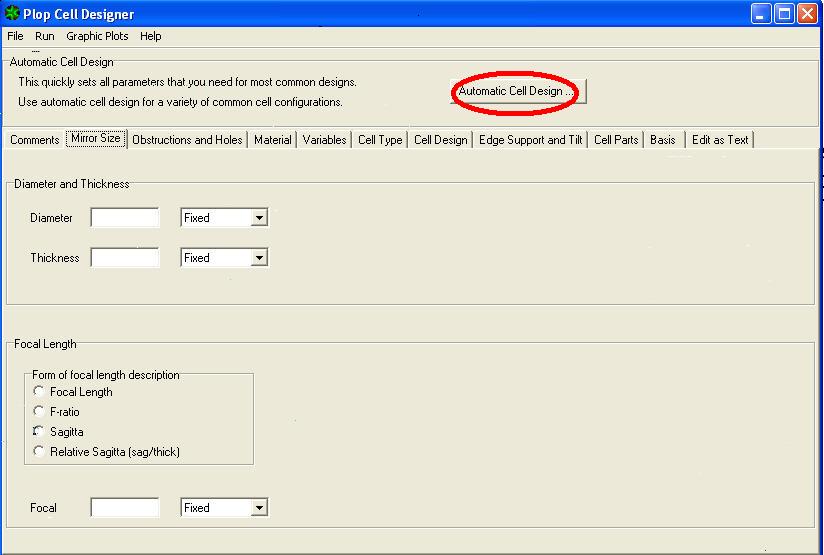
1) Nella finestra PLOP CELL DESIGNER cliccare su AUTOMATIC CELL DESIGN –

   

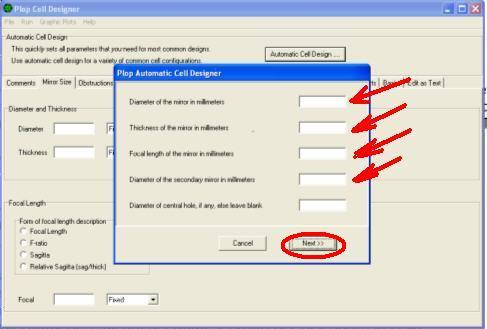
Si apre la finestra PLOP AUTOMATIC CELL DESIGNER, dove inserire diametro primario 300 mm – spessore 30mm – lunghezza focale 1500mm – diametro dello specchio secondario 67 mm – lasciare in bianco la casella foro centrale –

2) cliccare su NEXT –

  

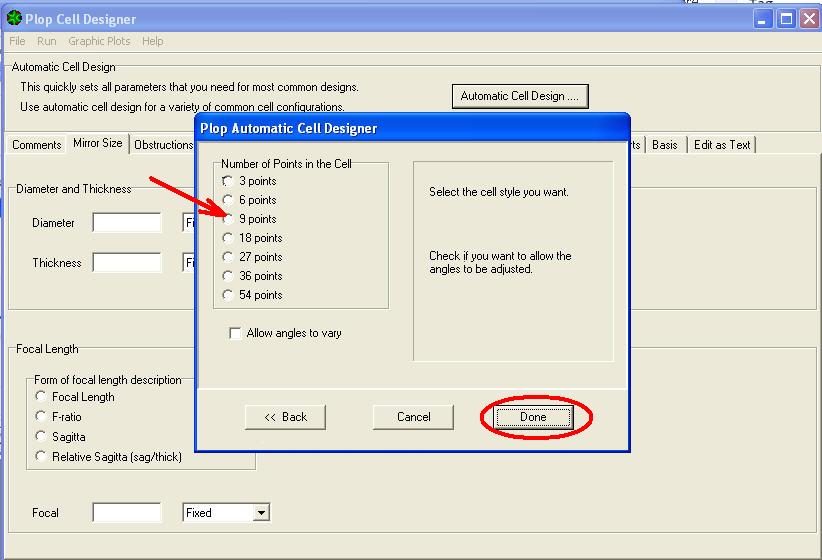
Si apre la finestra per la scelta del numero punti di appoggio della cella

3) Scegliere la cella a 9 punti e cliccare su DONE

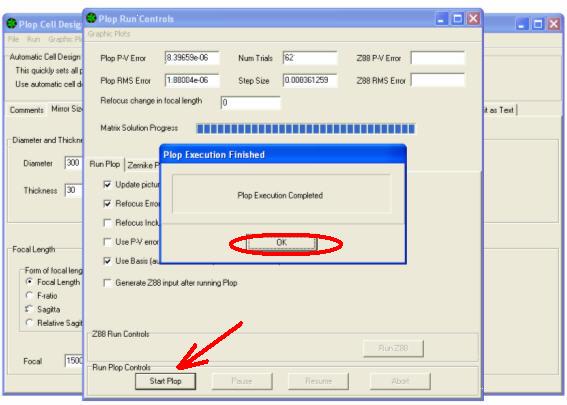
4) Si apre la finestra PLOP RUN CONTROLS in cui cliccare su START PLOT –

il programma elabora i calcoli e quando ha finito apre la finestra di comunicazione – PLOT EXECUTION FINISHED –

5) premere OK. Si rende visibile la seguente pagina , dalla quale, facendo clic sul separatore di schedario EDIT AS TEXT….

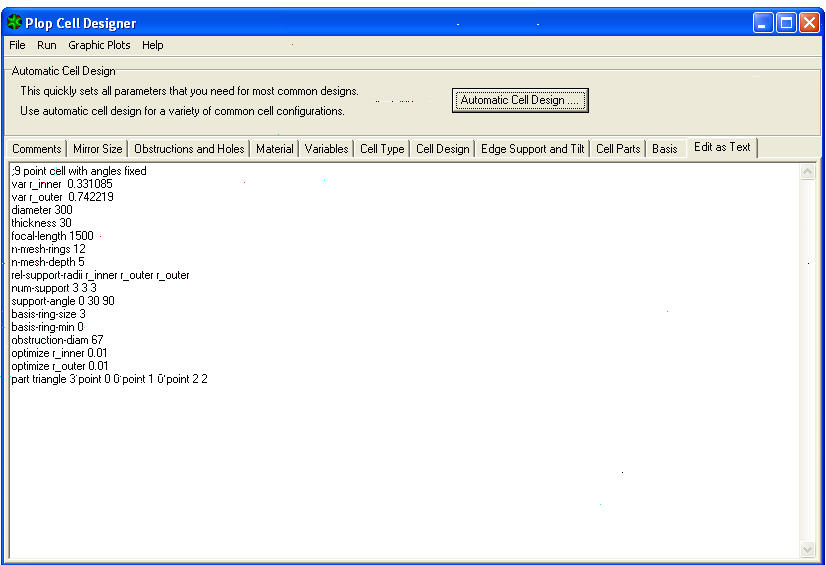
6) compare nella mezza pagina inferiore la seguente lista di variabili e relativi coefficienti di calcolo, che moltiplicati per il diametro specchio, forniscono le corrette misure delle circonferenze interna ed esterna, su cui sorgeranno (per la nostra cella a 9 punti) i 3 punti di appoggio interni, ed i 6 esterni dei triangoli di sostegno dello specchio nella sua cella.

  

7) Prepararsi a disegnare la cella con un CAD, o altro metodo di disegno manuale:

8) Innanzitutto disegnare il cerchio del diametro dello specchio primario (300mm);

9) Occorre ora cercare, fra le molte righe incolonnate relative alle variabili visualizzate, quella che ci permetterà di calcolare il raggio del cerchio di supporto interno, che è la  VAR R_INNER 0.331085 – e quindi moltiplicare il raggio dello specchio per quel coefficiente 0.331085 per ottenere il raggio del cerchio interno della cella su cui staranno i 3 punti di appoggio interni, della nostra cella a 9 punti.

(150×0.331085=) 49.66mm = raggio del cerchio di appoggi interno

10) Disegnare quel cerchio concentrico al diametro specchio.

11) Fra le stesse righe incolonnate cercare poi la variabile del raggio esterno VAR R_OUTER 0.742219 – e moltiplicare il raggio dello specchio per quel coefficiente per ottenere il raggio del cerchio su cui sono presenti altri punti di appoggio.

(150×0.742219=) 111.33mm = raggio del cerchio di appoggi esterno.

12) Disegnare questo cerchio concentrico ai precedenti.

13) Andare sul MENU’ della finestra PLOP CELL DESIGNER, e cliccare su GRAPHIC PLOTS, poi cliccare su CELL PARTS:

 

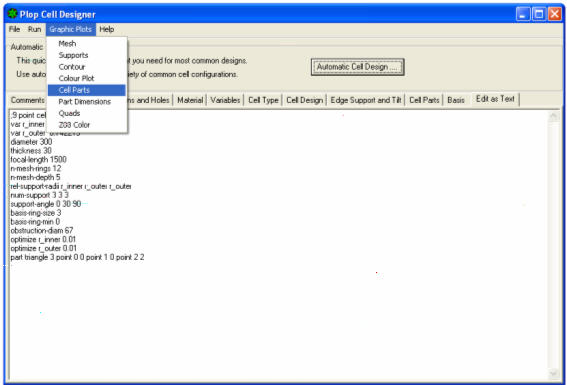
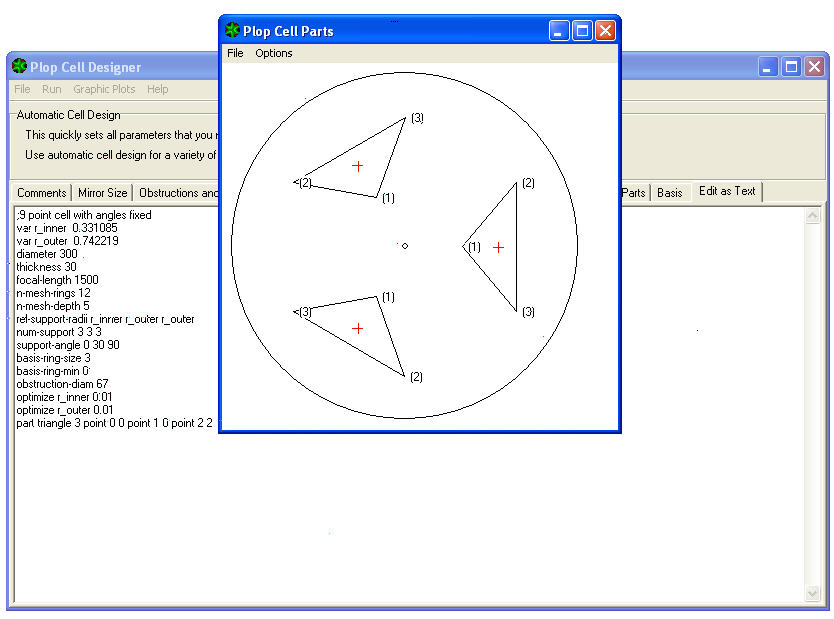
Si vedrà la posizione rispetto allo specchio dei tre triangoli isosceli di supporto (poiché è stata scelta una cella a 9 punti che appunto offre in appoggio i nove vertici dei tre triangoli).

 14) A questo punto, chiusa la finestrina PLOP CELL PART, siamo ancora sulla sottostante finestra che mostra l’elenco dei dati già utilizzati. Quindi per proseguire dobbiamo dapprima chiudere lo schedario EDIT AS TEXT, facendo clic su un altro schedario. Ad esempio sul vicino BASIS, al fine di evitare la comparsa di un errore bloccante “invalid floating point operation”l

Errore che è dovuto ad una incongruenza fra il segno virgola, usato da Windowws come separatore dei decimali in Italia, al posto del punto, separatore anglosassone richiesto nei calcoli del programma GUI PLOP.

Calcoli che dobbiamo rilanciare senza più visualizzarli, per evitare l’errore conseguente a quella sostituzione di separatore decimale.

15) Sulla finestra PLOP CELL DESIGNER facciamo clic sul pulsante AUTOMATIC CELL DESIGN, confermiamo con DONE gli stessi dati precedentemente introdotti nella scheda RUN CONTROL lanciando START PLOP , e premendo OK ad esecuzione completata

16) Occorre poi chiudere PLOP RUN CONTROL tornando alla finestra sottostante PLOP CELL DESIGNER, dal cui menù a tendina GRAPHIC PLOTS scegliere PART DIMENSIONS. 

  

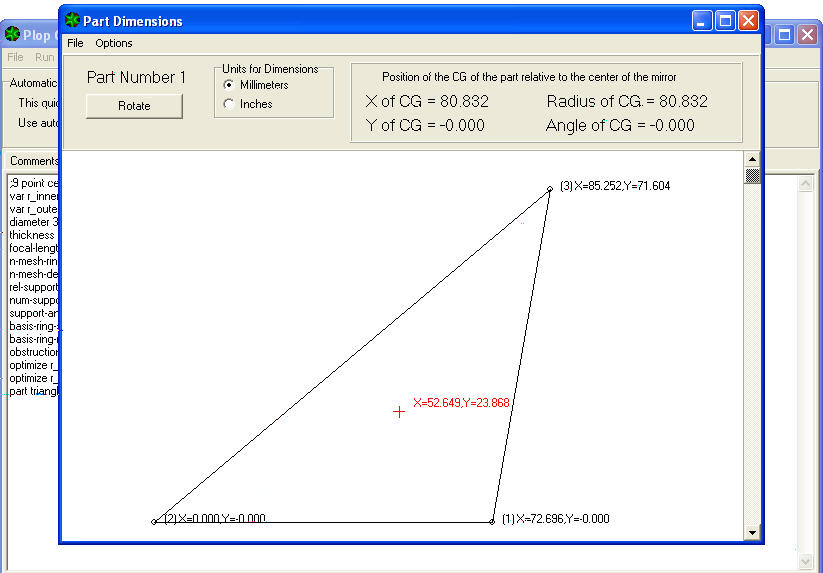
Compare la scheda dati della PART NUMBER 1, che è uno dei tre triangoli uguali, con le coordinate cartesiane dei tre vertici di appoggio, e del baricentro di ogni triangolo,  il quale cadrà su una terza circonferenza ancora da disegnare, ed intermedia fra le due già disegnate per i punti di appoggio dello specchio.

LA CASELLA IN ALTO indica la posizione del baricentro (CG=Center of Gravity del pezzo visualizzato), dato in coordinate relative al centro dello specchio con:

coordinata X del baricentro = 80.832mm e  coordinata Y = 0:

Il che significa quel baricentro è sulla verticale (Y=0) del centro specchio, ad una distanza (di raggio) dal centro di 80.832mm (coord. Y):

Distanza che individua questo terzo cerchio su cui giaceranno, a 120 gradi di distanza l’uno dall’altro, i tre baricentri dei tre triangoli di supporto specchio.

17) Disegnare quindi il cerchio concentrico di raggio 80.332mm sede dei supporti dei tre triangoli.

Guardando ora la figura del triangolo visualizzato, notiamo che sia i vertici che il baricentro sono indicati in coordinate cartesiane riferite questa volta al punto 2 (vertice 2 in basso a sinistra) del triangolo, che ha coordinate X=0 e Y=0, che indica il “punto zero di partenza” delle misure indicate.

Il punto 1 (la retta inferiore orizzontale) ha quindi coordinata X=72.696 e Y=0 il che significa che è lungo 72.696mm quanto cioè la sua ascissa, senza variazioni di ordinata (perchè Y= zero).

18) Scriviamo quel valore per non dimenticarlo.

La finestra col triangolo visualizzato, presenta il pulsante della funzione ROTATE, con la quale è possibile ruotare il triangolo in senso antiorario, e portare di volta in volta ognuno dei suoi tre vertici (il primo vertice era il numero 2; il secondo sarà il n.3 e il terzo il n. 1) nel punto – origine di coordinate X=0; Y=0,  che sta a sinistra della figura a video.

In questo modo, ad ogni rotazione che richiederemo, verrà via via visualizzata la lunghezza del lato che si trova orizzontale in basso, indicata dalla sua ascissa X.

19) Annotiamoci anche quei rimanenti due valori, che col primo identificano le dimensioni di ciascuno dei tre triangoli. (Due di tali tre valori saranno identici, perchè si tratta di triangoli isosceli).

20) Non resta quindi che disegnare i tre triangoli a 120° di distanza l’uno dall’altro, posizionando i 6 punti dei 9 complessivi, relativi agli estremi delle loro ipotenuse, sulla circonferenza di raggio ESTERNO (VAR R_OUTER =) 111.33mm;

E verificare che i tre punti relativi alle loro ALTEZZE andranno a giacere sulla circonferenza di raggio INTERNO (VAR R_INNER =) 49.66mm.

Mentre il loro baricentro si trova sulla circonferenza intermedia di raggio 80.832mm

PRENDERE NOTA CHE: In questo esempio relativo a una semplice cella a 9 punti, la CELL PART è una sola, cioè costituita dal triangolo di appoggio dello specchio (in questo caso da realizzare in tre esemplari identici).

Mentre se si scegliesse una cella a 18 punti, le CELL PARTS sarebbero due: Cioè come parte 1 vi sarà il triangolo di appoggio dello specchio, (in questo caso da realizzare in 6 esemplari identici) e come parte 2 la barra bilanciere che sostiene ciascuna delle tre coppie di triangoli (da realizzare in tre esemplari).

E così pure per altre celle complicate da maggiori punti di appoggio, la visualizzazione dei dati relativi alle ulteriori CELL PARTS si ottiene proseguendo oltre la visualizzazione dell’elemento numero uno (che è solitamente uno dei triangoli di appoggio dello specchio), facendo col mouse scorrere verso il basso il cursore che sta alla destra della finestra che visualizza del triangolo stesso. Apparirà così ogni ulteriore elemento costruttivo, con le solite modalità, riportante tutte le indicazioni nel box in alto della sua posizione, e a centro finestra delle sue dimensioni, che possono essere eventualmente riferite alle coordinate cartesiane dell’elemento che sta alla base del disegno, ruotabile come descritto nel caso del triangolo in questo tutorial riferito a una cella a 9 punti, per identificare i dati di volta in volta relativi al lato che si trova in posizione orizzontale.

FINE DEL DISEGNO DELLA CELLA.

Se ora torniamo al punto 13) PLOP CELL DESIGNER, e facciamo clic su GRAPHIC PLOTS, abbiamo la possibilità di scegliere di vedere altre rappresentazioni grafiche dello specchio e delle deformazioni che lo affliggeranno quando sarà montato sulla cella progettata.

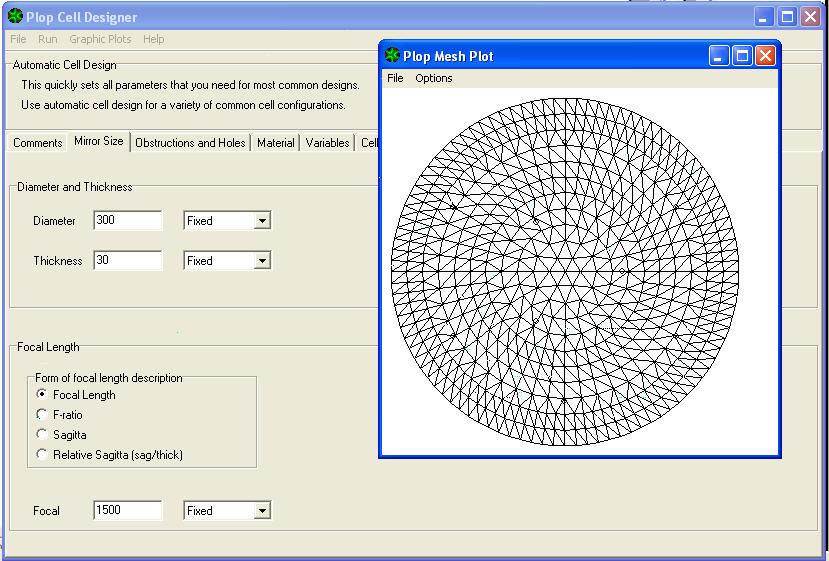
La prima visualizzazione possibile si ottiene cliccando sulla voce  MESH del menù a tendina GRAPHIC PLOTS, per vedere come la superficie dello specchio è stata suddivisa nella rete di poligoni di uguale area, individuati come gli “Elementi finiti” presi in considerazione nel calcolo.

La seconda voce del menù a tendina è SUPPORTS, e l’avevamo già vista più sopra.

La terza voce del menù a tendina è CONTOUR e mostrerà le linee di livello delle sollecitazioni attorno ai punti d’appoggio. Una sorta di linee isoipse che indicano le omogenee variazioni del livello (seppure infinitesimo) raggiunto dalla superficie deformata, a parità di sollecitazione.

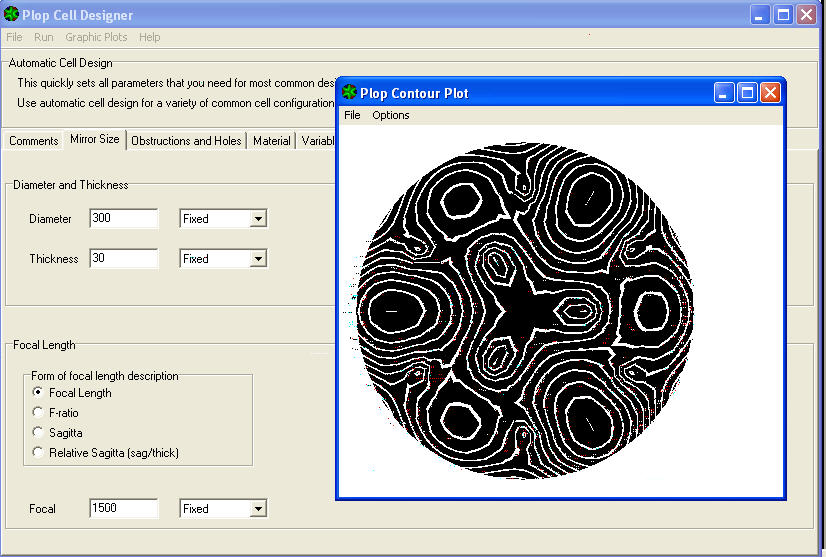
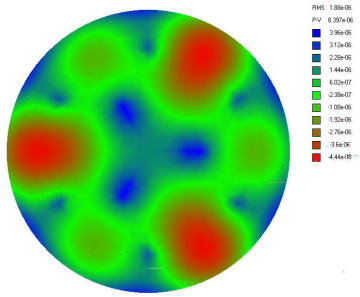
La quarta voce del menù a tendina è la interessante COLOURPLOT che mostrerà la mappa con la quantità delle deformazioni espresse SIA in rapporto RMS come “valore efficace” relativo alla intera superficie, CHE  a livello locale nei vari colori di una scala indicata a lato, indicante valori PICCO/VALLE delle deformazioni  generate.

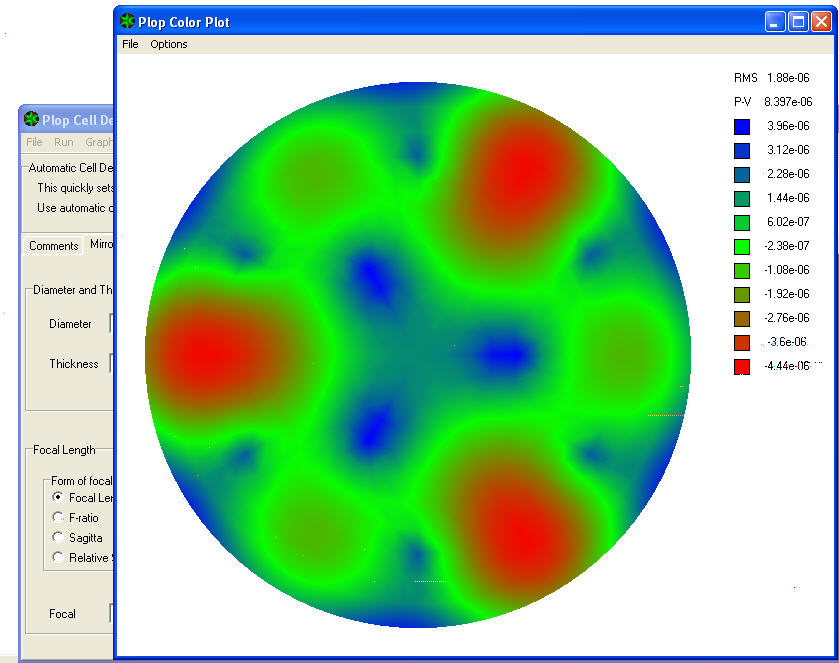
Il valore RMS 1.88E-06 rilevabile nella colonna più in alto a destra del grafico, indica il valore efficace (o quadratico medio) dell’errore prodotto sulla intera superficie dello specchio da questo tipo di cella, in rapporto alla lunghezza d’onda (lambda) di 550 nanometri della luce giallo-verde a cui l’occhio umano è più sensibile;

Mentre il sottostante valore P-V 8.397E-06 indica l’errore espresso come picco/valle, ovvero minimo e massimo locali della superficie.

In pratica le zone in colore azzurro sono quelle meno deformate sostenute bene dai punti di appoggio dei sostegni dello specchio; mentre le zone verdi sono di deformazione intermedia, e quelle rosse sono quelle maggiormente deformate.

Come farsi una idea della bontà della cella?

Anche senza ricorrere alla matematica per una quantificazione tecnica precisa, leggiamo sul testo guida del programma  “plop user.pdf”, il suggerimento che un errore RMS di 4.2E-06 mm corrispondente a Lambda/128, è da considerarsi un limite ragionevolmente buono per una cella.

La nostra cella denuncia nel grafico un valore RMS di 1.88E-06, che è 2.23 volte più piccolo e quindi migliore, del limite indicato come ragionevolmente buono per una cella.

Ora che ci siamo fatti una idea dell’ordine di grandezza della qualità della nostra cella, vediamo solo a cosa servono le rimanenti voci del menù a tendina.

Proseguiamo e finiamo saltando la quinta e la sesta voce CELL PARTS e PART DIMENSIONS, perchè sono ambedue già state viste più sopra, ed incontriamo l’ultima voce “Z88” del menù a tendina, la quale non è di nostro diretto interesse poichè si riferisce all’uso di una estensione software denominata Z88 per “addetti ai lavori” del calcolo con gli elementi finiti.