PERCHE’ STUDIARE QUEL CHE IL SOFTWARE CI OFFRE GIA’ PRONTO ALL’USO
Lo studio dei risultati del test di Foucault è molto importante per poter valutare bene e autonomamente i consigli forniti dai software predisposti per tale calcolo. Nessuno è perfetto e nemmeno i programmi per questi calcoli lo sono, pur essendo in grado di guidarci ugualmente alla meta.
Siccome le alternative per arrivare a quella meta possono essere molte se non infinite, vale la pena di usare il nostro proprio senso critico opportunamente preparato, per non accettare ciecamente il verdetto del software.
Nel nostro percorso di lettura degli articoli precedenti abbiamo intuito che nella realizzazione di uno specchio parabolico si procede per piccoli passi, non essendo tecnicamente possibile produrre la parabolizzazione della superficie sferica di vetro in un solo colpo.
Nel precedente articolo abbiamo visto in che modo viene condotto il test di Foucault, sulla base del quale possono venire calcolate manualmente le valutazioni della superficie, allo scopo di decidere quale ritocco intraprendere nella prossima correzione.
Vediamo ora come un programma di elaborazione informatica avrebbe elaborato gli stessi “tiraggi” rilevati col Foucault e utilizzati nel precedente calcolo manuale.
Faccio quindi riferimento alle parti di un foglio di excel da me tradotto e adattato, che è reperibile nella sua forma originale all’indirizzo indicato sul foglio medesimo.
Utilizzo questo foglio di preferenza, per il fatto che pur offrendomi la “SUA” soluzione migliore, mi permette di simulare altre vie personali, e di prevederne i risultati. Cosa questa che altri più rigidi programmi di gestione del test di Foucault non permettono con la flessibilità di un foglio di calcolo.
Vediamo quindi:
UN CALCOLO INFORMATICO DEL TEST DI FOUCAULT
Troviamo nella figura 1 che sono stati inseriti in casella E,F,G,H 27, i seguenti dati dei quattro tiraggi riferiti alle 4 zone dello specchio in esame
| 31.00 | 31.50 | 31.80 | 32.00 |
Sappiamo già che per verificare l’andamento della curva parabolica grezza che stiamo costruendo, dovremmo “sovrapporla” alla perfetta parabola di riferimento mettendo le due curve a diretto contatto, e pure diretto confronto, in un punto comune, che può essere qualunque punto “hm” della nostra curva preso lungo il raggio dello specchio.
Questo ci permetterà di vedere, a seconda del “punto di contatto” scelto, quali siano le deviazioni assunte dalla nostra curva rispetto a quella di riferimento, per stabilire quale sia la condizione più favorevole ad una correzione che ci porti nel prosieguo del lavoro, ad avvicinarci il più possibile alla parabola di riferimento.
Quella sovrapposizione pratica delle due curve la simuliamo perfettamente con i numeri, mediante la sottrazione a tutte le zone misurate, di una opportuna costante (di distanza) che porta a zero il valore di tiraggio in UN PUNTO preso come contatto reciproco.
E proprio quella sottrazione di quel medesimo valore a tutte le zone, simulerà il movimento di sovrapposizione delle due curve, della cui qualità vedremo un immediato risultato dai grafici.
Ricordiamo quindi che la parola “aberrazione” è un termine tecnico che in realtà indica il grado di deformazione che la nostra parabola ha in quel punto, rispetto alla sfera di origine. (oppure deve avere, se quell’aberrazione è riferita alla parabola di riferimento).
L’aberrazione di una zona, in altre parole, esprime i millimetri di diversità di tiraggio che dovremmo trovare in quella zona perchè la nostra parabola sia identica a quella di riferimento.
E ricordando ancora di più, che il raggio di curvatura R è un derivato della lunghezza focale realmente misurata, che è la base su cui vengono calcolate le aberrazioni della parabola di riferimento: Diventa di fondamentale importanza che il valore della lunghezza focale venga misurato, controllato ed aggiornato nel foglio di calcolo, ogni volta che si presume che essa possa essere cambiata anche di pochissimo in seguito a ritocchi di correzione che coinvolgono il centro specchio.
Calcoliamo quindi per ogni zona, la “costante” di distanza che separerebbe le due curve, come differenza fra i nostri tiraggi (che sono le reali aberrazioni della nostra parabola in costruzione) con le aberrazioni hm2/R. proprie della parabola di riferimento.
Sottraiamo quindi ai valori delle zone 1,2,3,4,
| 31.00 | 31.50 | 31.80 | 32.00 |
Le aberrazioni hm2/R. di riferimento:
| 0.145 | 1.080 | 2.282 | 3.469 |
Ed otterremo le seguenti possibili quattro costanti di sovrapposizione da provare una ad una:
| 30.86 | 30.42 | 29.52 | 28.53 |
Vediamo quindi quel che succederebbe alla nostra curva parabolica in costruzione, sovrapponendola in quattro modi diversi, uno per ogni zona, alla parabola di ferimento:
CONTATTO IN ZONA 1
Se ora proviamo a sovrapporre la costante 30.86 simulando il contatto sulla prima zona, inserendo il valore 30.86 nella casella I28 “valore ritenuto”. Il grafico seguente indica quali correzioni, e di che entità, andrebbero apportate alle zone 2,3 e4, per ottenere la parabola di riferimento.
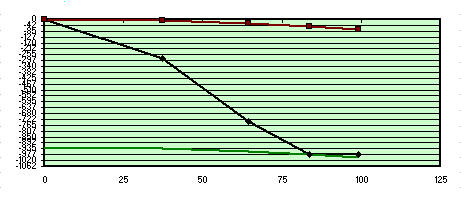
Aberrazioni riferite alla zona 1
Prendendo per buona la zona 1 (che infatti si vede perfettamente sovrapposta alla parabola bassa in colore verde, che con la rossa superiore esprime la distanza picco – valle del massimo difetto in lambda/0.5) Ci troveremmo a parabolizzare per il bordo: cioè ci troveremmo in condizioni molto sfavorevoli, ad avere un bordo estremamente rialzato con la necessità di asportare quasi 500 nanometri di vetro in zona 4 e 3, il che vorrebbe dire troppo lavoro.
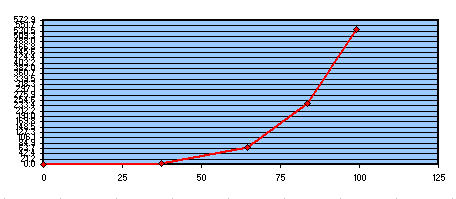
Vetro da asportare per ottenere la parabola di riferimento tenendo buona la zona 1
CONTATTO IN ZONA 2:
Proviamo ora a sovrapporre in zona 2, utilizzando la costante 30.42 in casella I28. Il grafico seguente indica quali correzioni, e di che entità, andrebbero apportate alle zone 1, 3 e 4 per ottenere la parabola di riferimento.
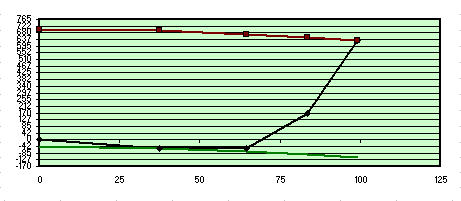
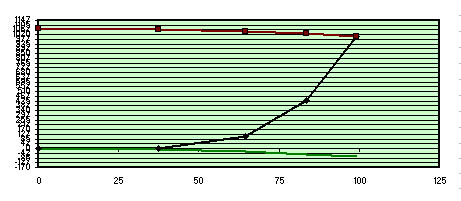
Aberrazioni riferite alla zona 2
Prendendo per buona la zona 2 (che infatti si vede perfettamente sovrapposta alla parabola bassa in colore verde, che con la rossa superiore esprime la distanza picco – valle del massimo difetto contenuto in lambda/0.8) ci troveremmo ancora a parabolizzare per il bordo, quindi in condizioni sfavorevoli seppure un poco migliori dalle precedenti, in quanto avremmo la zona 1 di 21,2 nanometri leggermente più alta della perfezione; ma continueremmo ad avere le zone 3 e 4 molto alte, con una quantità di vetro da asportare di circa 362 nanometri complessivi in zona 4 e 3. Il che vorrebbe dire troppo lavoro.
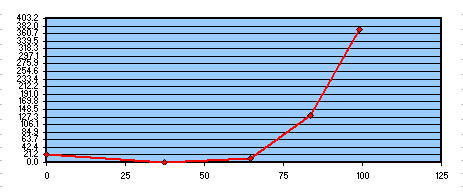
Vetro da asportare per ottenere la parabola di riferimento tenendo buona la zona 2
CONTATTO IN ZONA 3:
Proviamo ora a sovrapporre in zona 3, utilizzando la costante 29.52 in casella I28
Il grafico seguente indica quali correzioni, e di che entità, andrebbero apportate alle zone 1, 2 e 4 per ottenere la parabola di riferimento.
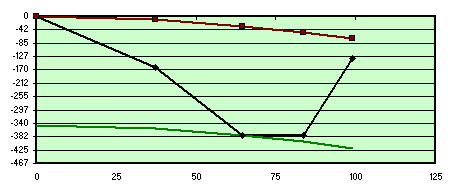
Aberrazioni riferite alla zona 3
Prendendo per buona la zona 3 (che infatti si vede sovrapposta alla parabola bassa in colore verde, che con la rossa superiore esprime la distanza picco – valle del massimo difetto in lambda/1.6) ci troveremmo a parabolizzare per il 70% del diametro; ci troveremmo in buone condizioni, in quanto avremmo le zone 1 e 2 e 4 “alte” complessivamente, ma facili da “abbassare” . al momento senza rischio, con un occhio di riguardo alla zona 4 per evitare di lavorarla troppo e male, ed ottenere da un bel bordo rilevato un brutto bordo ribattuto impossibile da correggere senza tornare indietro verso la sfera.
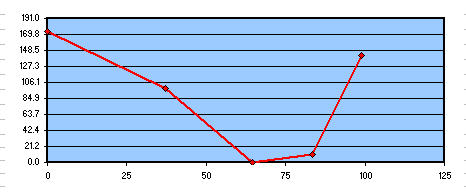
Vetro da asportare per ottenere la parabola di riferimento tenendo buona la zona 3
CONTATTO IN ZONA 4:
Proviamo ora a sovrapporre in zona 4, utilizzando la costante 28.53 in casella I28
Il grafico seguente indica quali correzioni, e di che entità, andrebbero apportate alle zone 1, 2 e 3 per ottenere la parabola di riferimento.
Prendendo per buona la zona 4 (che infatti si vede sovrapposta alla parabola bassa in colore verde, che con la rossa superiore esprime la distanza picco – valle del massimo difetto in lambda/0.6) ci troveremmo a parabolizzare per il centro specchio, ovvero ci troveremmo a dover scegliere fra due interessanti casi:
- la “cattiva” condizione della zona centrale dello specchio, data dal fatto che avremmo le zone 1,2 e 3, da scavare di ben 462 nanometri, il che, non sarebbe conveniente alla luce del maggior tempo di lavoro che dovremmo fare, seppure con ampie tolleranze di lavorazione .
- la “ottima” condizione di quella zona 4 di bordo specchio già perfetta, in cui vi sono tolleranze ristrettissime di lavorazione. Ottima e allettante perchè, quel lungo lavoro di abbassamento delle zone 1,2,3 centrali lontane dal bordo specchio e con tolleranza di lavorazione molto ampia, si svolgerebbe lontano dal bordo specchio e assolutamente senza rischio di ottenere un bordo ribattuto.
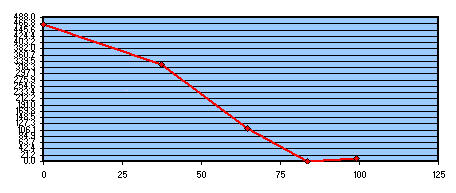
Vetro da asportare per ottenere la parabola di riferimento tenendo buona la zona 4
Queste quattro diverse sovrapposizioni, sono un esempio della variabilità del lavoro richiesto prendendo come riferimento punti diversi, che noi per semplicità abbiamo considerato il centro delle nostre quattro zone.
CONTATTO NEL PUNTO SUGGERITO DAL SOFTWARE INDICATO IN FIGURA 1:
Nonostante le nostre variazioni sul tema, le formule contenute nel foglio hanno prodotto automaticamente una variabile di 29.831mm, frutto della somma delle nostre quattro misure alla quale è stata sottratta la somma delle quattro aberrazioni di riferimento, mediando infine tale risultato dividendolo per 4 quante sono le zone, col risultato grafico seguente:
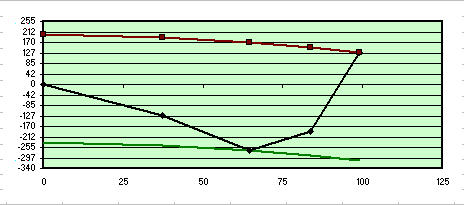
Aberrazioni riferite alla zona calcolata dal foglio
Prendendo per buona la costante del software 29.83, che indica un punto fra la zona 2 e la 3, (che infatti si vede quel punto sovrapposto alla parabola bassa in colore verde, che con la rossa superiore esprime la distanza picco – valle del massimo difetto in lambda/1.3) ci troveremmo a parabolizzare all’incirca per il 70% diametro, cioè ci troveremmo in buone condizioni, pur se di uno 0.3 peggiori di quelle della nostra simulazione sul contatto in zona 3. Ma a questo punto della lavorazione sostanzialmente equivalenti a quelle della nostra simulazione sul contatto in Zona 3, in quanto avremmo le zone 1 e 2 “alte” complessivamente, ma facili da “abbassare” , con una zona 4 più alta rispetto alla nostra simulazione, e al momento senza rischio.
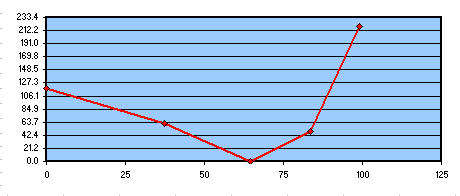
Vetro da asportare per ottenere la parabola di riferimento tenendo buono il punto di contatto suggerito dal foglio
COSA SI VUOLE DIMOSTRARE CON TUTTO CIO?
L’apparente inutilità di questo ragionamento accademico serve a prendere dimestichezza con le infinite vie che portano alla parabolizzazione di uno specchio perfetto, il cui risultato dipende solo dalla costanza di chi lo lavora, e dall’aver capito quel che sta dietro ai rigidi e comodi risultati forniti dai software predisposti per il test di Foucault, e dal non prendere e subire tali risultati in modo acritico.
Simulando manualmente può succedere che si trovi una via “ancora migliore della migliore”, per raggiungere un risultato ottimo in condizioni impensabili senza simulazione.
la simulazione è potente e non va relegata solo alle possibilità date dalle zone e indicate in questo articolo, ma può essere molto utile soprattutto per provare a cambiare valori di tiraggio in una o più zone, coerentemente e verosimilmente con la prossima azione di correzione che abbiamo già deciso di intraprendere, per giudicare con i nostri occhi se quel che succederebbe è buono, e di quanto lo è.
Succede infatti che praticando le simulazioni uno si renda conto che con una leggera azione potrebbe ottenere a sorpresa un lambda a due cifre, altrimenti non immaginabile.